Calculating the period of the sunspot cycle

Two weeks ago, I used the sunspot number data provided by the Solar Physics Group at NASA's Marshall Space Flight Center to demonstrate positioning plots in window. This week, I'd like to show how to calculate the period of the sunspot cycle. If you haven't already done so, download the sunspot numbers file and place it in your IDL path. Read it with the astrolib READCOL procedure:

 file = file_which('spot_num.txt', /include) readcol, file, year, month, sunspots

Next, transform the sunspot series to the frequency domain and compute magnitude and power spectra:

 mspec = abs(fft(sunspots)) pspec = mspec^2

(Aside: FFT: it's all you need.) I'd like to display the power spectrum as a function of frequency. This requires a few statements to set up a frequency vector based on the time data from the sunspot numbers file:

 sampling_interval = 1/12.0 ; years, from file freq_nyquist = 0.5/sampling_interval ; years^{-1} n_sunspots = n_elements(sunspots) freq = findgen(n_sunspots/2)/(n_sunspots/2-1)*freq_nyquist

The sampling interval is one month. This allows me to determine the Nyquist frequency (the maximum resolvable frequency), which along with the number of sunspots in the file, gives me the information to define a frequency vector. Note that I'm defining only positive frequencies up to the Nyquist frequency; this is because I'm going to display a one-sided power spectrum. Fold the negative Fourier modes into the spectrum, omitting the zero (DC) mode:

 freq_nodc = freq[1:n_sunspots/2-1] pspec_nodc = 2*pspec[1:n_sunspots/2-1]

and display the result on logarithmic axes:

 p = plot(freq_nodc, pspec_nodc, /xlog, /ylog, $ xtickunits='exponent', $   ; IDL 8.2.1 xtitle='Frequency ($yr^{-1}$)', $ ytitle='Spectral Density', $ title='Power Spectrum of Sunspot Numbers, 1749-2010')

Note that I can set the style of tick units on the axes: 'exponent' and 'scientific' are new in IDL 8.2.1. The power spectrum has a peak near 0.1 yr^{-1}. Locate the peak frequency with MAX and mark it on the plot with POLYLINE:

 pspec_nodc_peak = max(pspec_nodc, i_peak) freq_nodc_peak = freq_nodc[i_peak] !null = polyline([1.0,1.0]*freq_nodc_peak, p.yrange, color='orange', /data)

The inverse of the peak frequency gives the period of the sunspot cycle: approximately 11 years. Mark this on the plot with TEXT:

 sunspot_peak_period = 1.0/freq_nodc_peak str = '$T_{peak}$ = ' + strtrim(sunspot_peak_period,2) + ' years' !null = text(1e-1, 1e-4, str, /data)

Here's my result:

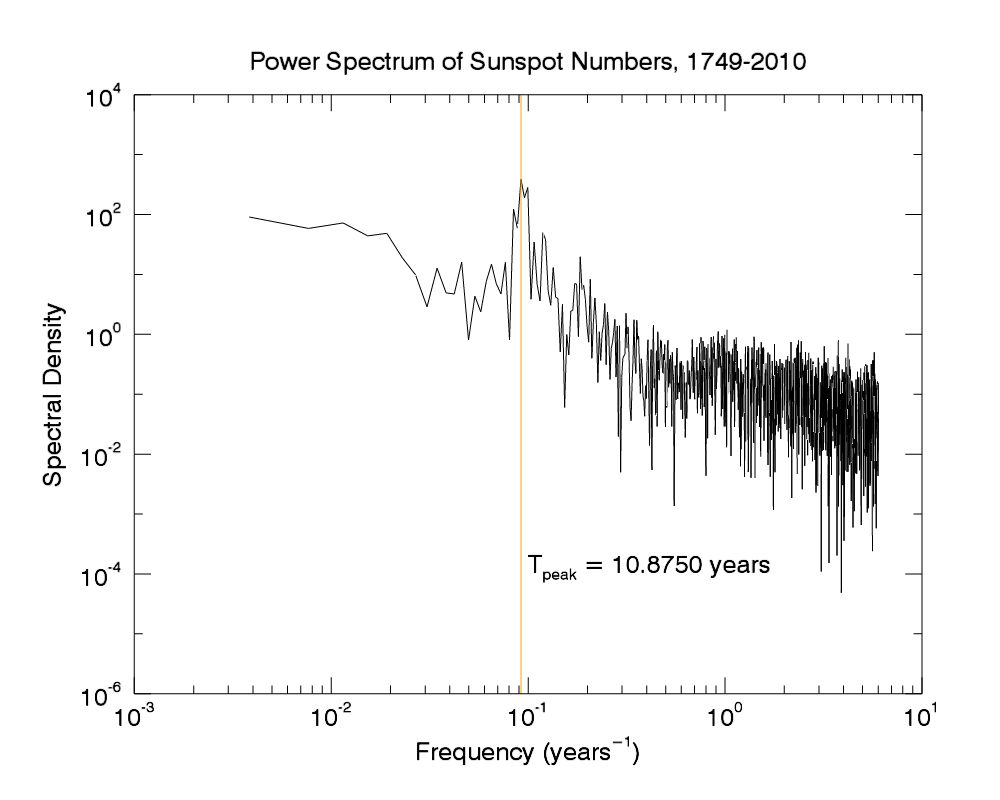
Finally, just because it's interesting, test Parseval's theorem (energy is conserved in the time- and frequency-domain representations of the signal) in several forms:

 IDL> print, total(pspec)*n_sunspots, total(sunspots^2) 1.46437e+007 1.46437e+007 IDL> print, mspec[0], mean(sunspots) 52.0133      52.0134 IDL> print, total(pspec[1:*]), stddev(sunspots)^2*(n_sunspots-1)/n_sunspots ; convert from sample variance 1965.67      1965.66

Conservation of greatness (of FFT)!