The FZ_ROOTS function is used to find the roots of an m-degree complex polynomial, using Laguerre’s method.
FZ_ROOTS is based on the routine zroots described in section 9.5 of Numerical Recipes in C: The Art of Scientific Computing (Second Edition), published by Cambridge University Press, and is used by permission.
Examples
Example 1: Real coefficients yielding real roots.
Find the roots of the polynomial:
P (x) = 6x3 - 7x2 - 9x - 2
The exact roots are -1/2, -1/3, 2.0.
coeffs = [-2.0, -9.0, -7.0, 6.0]
roots = FZ_ROOTS(coeffs)
PRINT, roots
IDL prints:
( -0.500000, 0.00000)( -0.333333, 0.00000)( 2.00000, 0.00000)
See Additional Examples for more information on using FZ_ROOTS.
Syntax
Result = FZ_ROOTS(C [, /DOUBLE] [, EPS=value] [, /NO_POLISH] )
Return Value
Returns an m-element complex vector containing the roots of an m-degree complex polynomial.
Arguments
C
A vector of length m+1 containing the coefficients of the polynomial, in ascending order (see example). The type can be real or complex.
Keywords
DOUBLE
Set this keyword to force the computation to be done in double-precision arithmetic.
EPS
The desired fractional accuracy. The default value is 2.0 x 10-6.
NO_POLISH
Set this keyword to suppress the usual polishing of the roots by Laguerre’s method.
Additional Examples
Example 2: Real coefficients yielding complex roots.
Find the roots of the polynomial:
P (x) = x4 + 3x2 + 2
The exact roots are:
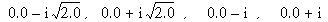
coeffs = [2.0, 0.0, 3.0, 0.0, 1.0]
roots = FZ_ROOTS(coeffs)
PRINT, roots
IDL Prints:
(0.00000, -1.41421)(0.00000, 1.41421)
(0.00000, -1.00000)(0.00000, 1.00000)
Example 3: Real and complex coefficients yielding real and complex roots.
Find the roots of the polynomial:
P (x) = x3 + (-4 - i4)x2 + s (-3 + i4)x + (18 + i24)
The exact roots are –2.0, 3.0, (3.0 + i4.0)
coeffs = [COMPLEX(18,24), COMPLEX(-3,4), COMPLEX(-4,-4), 1.0]
roots = FZ_ROOTS(coeffs)
PRINT, roots
IDL Prints:
( -2.00000, 0.00000) ( 3.00000, 0.00000) ( 3.00000, 4.00000)
Version History
See Also
FX_ROOT, BROYDEN, NEWTON, POLY