GAMMA

The GAMMA function returns the gamma function of Z.

The gamma function is defined as:

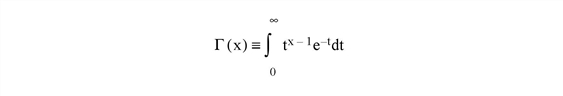
Use the LNGAMMA function to obtain the natural logarithm of the gamma function when there is a possibility of overflow.

Examples

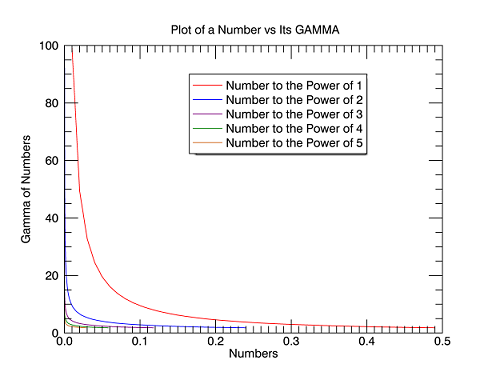
Plot the gamma function over the range 0 to 0.5:

; Generate the numbers to use in the GAMMA function.

Z = FINDGEN(50)/100.

; Plot the GAMMA of each of these numbers.

p1 = PLOT(Z, GAMMA(Z), XTITLE='Numbers', $

   YTITLE='Gamma of Numbers', COLOR='red', $

   TITLE="Plot of a Number vs Its GAMMA", $

   NAME='Number to the Power of 1')

; Plot the GAMMA of the numbers vs the number

; raised to one of several exponents.

p1 = PLOT((Z^2), GAMMA(Z), COLOR='blue', $

   NAME='Number to the Power of 2', /OVERPLOT)

p1 = PLOT((Z^3), GAMMA(Z), COLOR='purple', $

   NAME='Number to the Power of 3', /OVERPLOT)

p1 = PLOT((Z^4), GAMMA(Z), COLOR='green', $

   NAME='Number to the Power of 4', /OVERPLOT)

p1 = PLOT((Z^5), GAMMA(Z), COLOR='chocolate', $

   NAME='Number to the Power of 5', /OVERPLOT)

L = LEGEND(POSITION=[0.4,90], /DATA)

Syntax

Result = GAMMA(Z)

Return Value

If Z is double-precision, the result is double-precision (either double or double complex), otherwise the result is single-precision (either float or complex).

Arguments

Z

The expression for which the gamma function will be evaluated. Z may be complex.

Keywords

Thread Pool Keywords

This routine is written to make use of IDL’s thread pool, which can increase execution speed on systems with multiple CPUs. The values stored in the !CPU system variable control whether IDL uses the thread pool for a given computation. In addition, you can use the thread pool keywords TPOOL_MAX_ELTS, TPOOL_MIN_ELTS, and TPOOL_NOTHREAD to override the defaults established by !CPU for a single invocation of this routine. See Thread Pool Keywords for details.

Version History

Original	Introduced
5.6	Z argument accepts complex input