The LAMBERTW function returns the value W(z) of the Lambert W function, also known as the omega function or product logarithm function. The defining equation is given by:
z = W(z) eW(z)
where z is any complex number. Because the equation has an infinite number of solutions for each z, there are an infinite number of branches. By default LAMBERTW returns the principal branch of the equation, but you can also pass in an optional branch parameter k.
The Lambert W function has many applications in mathematics, computer science, and the physical sciences. It is used in the enumeration of trees, when solving equations with exponentials (such as the maxima of the Bose-Einstein or Fermi-Dirac distributions), or in the solution of linear constant-coefficient delay equations. It is also closely related to the tree function, with T(z) = –W(–z).
This routine is written in the IDL language. Its source code can be found in the file lambertw.pro in the lib subdirectory of the IDL distribution.
The routine uses Halley's method to find the solution, with an initial guess based upon the series expansion:
W(z) = L – M + M/L + M(M–2)/(2L2) + M(6 – 9M + 2M2)/(6L3)
For the principal branch, L = log(z) and M=log(L). For other branches, L=log(z) + 2∏ik and M=log(L).
Examples
Example 1
Compute the value of the Lambert W function at the following X values:
x = [-0.3d, -0.2d, -0.1d, 0, 0.1d, 0.2d, 0.3d]
result = LAMBERTW(x)
PRINT, result
IDL prints:
-0.48940223 -0.25917110 -0.11183256 0.00000000 0.091276527 0.16891597 0.23675531
For the negative values, also compute the lower branch:
x = [-0.3d, -0.2d, -0.1d, 0]
result = LAMBERTW(x, /LOWER_BRANCH)
PRINT, result
IDL prints:
-1.7813370 -2.5426414 -3.5771521 -Infinity
Example 2
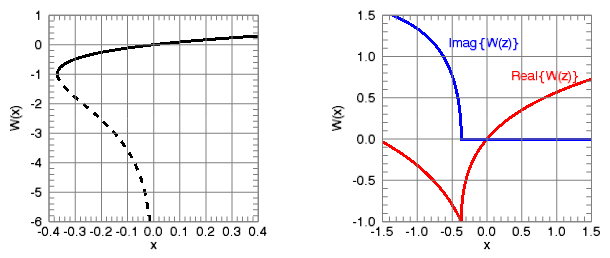
Plot both the principal and lower branch of the real-valued Lambert W function:
p1 = PLOT('LambertW(x)', '3', LAYOUT=[2,1,1], $
XTITLE='x', YTITLE='W(x)', $
XRANGE=[-0.4,0.4], YRANGE=[-6,1], DIMENSIONS=[800,300], $
XMAJOR=9, XTICKLEN=0.5, XSUBTICKLEN=0.05, XMINOR=4, $
YTICKLEN=0.5, YSUBTICKLEN=0.05, YMINOR=4, $
XCOLOR='gray', YCOLOR='gray', $
XTEXT_COLOR='black', YTEXT_COLOR='black')
p2 = PLOT('LambertW(x, /LOWER_BRANCH)', '3--', $
/OVERPLOT)
Plot the real and imaginary parts for the principal value with complex Z:
p3 = PLOT('REAL_PART(LambertW(DCOMPLEX(x)))', '3r', $
LAYOUT=[2,1,2], /CURRENT, $
XTITLE='x', YTITLE='W(x)', $
XRANGE=[-1.5,1.5], YRANGE=[-1,1.5], $
XMAJOR=7, XTICKLEN=0.5, XSUBTICKLEN=0.05, $
YTICKLEN=0.5, YSUBTICKLEN=0.05, $
XCOLOR='gray', YCOLOR='gray', $
XTEXT_COLOR='black', YTEXT_COLOR='black')
p4 = PLOT('IMAGINARY(LambertW(DCOMPLEX(x)))', '3b', $
/OVERPLOT)
t = TEXT(0.35, 0.7, 'Real{W(z)}', /DATA, COLOR='red', TARGET=p3)
t = TEXT(-0.55, 1.1, 'Imag{W(z)}', /DATA, COLOR='blue', TARGET=p3)
Syntax
Result = LAMBERTW( Z [, K] [, /LOWER_BRANCH] )
Return Value
Single Argument
If Z is a scalar the result will be a scalar, otherwise the result will have the same dimensions as Z.
Both Arguments
If both Z and K are scalars, the function returns a scalar. If both arguments are arrays, the function matches up the corresponding elements of Z and K, returning an array with the same dimensions as the smallest array. If one argument is a scalar and the other argument is an array, the function uses the scalar value with each element of the array, and returns an array with the same dimensions as the smallest input array.
Result Type
If Z is type float or double and K is not specified then the result is double-precision.
If Z is type complex or dcomplex or K is specified then the result is double-complex.
Arguments
Z
The expression for which IDL should computer W(z). If Z is type float or double and you do not specify K, then the Z values should be greater than or equal to –EXP(–1) = –0.367879. Furthermore, if you set the LOWER_BRANCH keyword, the Z values should be between –EXP(–1) and 0. IDL will set the result for Z values outside of this range to the special value NaN.
K
An integer scalar or array specifying the branch k for W(z). If you do not specify K then the principal branch (k=0) is returned.
Keywords
LOWER_BRANCH
Set this keyword to force LAMBERTW to return the lower branch (k=–1) instead of the default upper branch. This keyword is only designed to work with float or double input in the range –EXP(–1) to 0. This keyword can not be used with complex input or with the K argument.
Version History
Resources and References
For more details on the Lambert W function, see Eqn. 4.18 in Corless, R. M., Gonnet, G. H., Hare, D. E. G., Jeffrey, D. J. and Knuth, D. E., 1996: On the Lambert W function, Advances in Computational Mathematics, 5, 329–359.
See Also
ALOG, EXP, PLOT