LA_LEAST_SQUARE

LA_LEAST_SQUARE_EQUALITY

The LA_LEAST_SQUARE_EQUALITY function is used to solve the linear least-squares problem:

Minimize_x||Ax - c||₂ with constraint Bx = d

where A is an n-column by m-row array, B is an n-column by p-row array, c is an m-element input vector, and d is an p-element input vector with p ≤ n ≤ m+p. If B has

full row rank p and the array 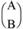has full column rank n, then a unique solution exists.

LA_ LEAST_SQUARE_EQUALITY is based on the following LAPACK routines:

Output Type	LAPACK Routine
Float	sgglse
Double	dgglse
Complex	cgglse
Double complex	zgglse

Examples

Given the following system of equations:

2t + 5u + 3v + 4w = 9

7t +  u + 3v + 5w = 1

4t + 3u + 6v + 2w = 2

with constraints,

-3t +  u + 2v + 4w = -4

 2t + 5u + 9v + 1w =  4

find the solution using the following code:

; Define the coefficient array:

a = [[2, 5, 3, 4], $

   [7, 1, 3, 5], $

   [4, 3, 6, 2]]

; Define the constraint array:

b = [[-3, 1, 2, 4], $

[2, 5, 9, 1]]

; Define the right-hand side vector c:

c = [9, 1, 2]

; Define the constraint right-hand side d:

d = [-4, 4]

; Find and print the minimum norm solution of a:

x = LA_LEAST_SQUARE_EQUALITY(a, b, c, d)

PRINT, 'LA_LEAST_SQUARE_EQUALITY solution:'

PRINT, x

IDL prints:

LA_LEAST_SQUARE_EQUALITY solution:

     0.651349      2.72695     -1.14638    -0.620036

Syntax

Result = LA_LEAST_SQUARE_EQUALITY( A, B, C, D [, /DOUBLE] [, RESIDUAL=variable] [, STATUS=variable] )

Return Value

The result (x) is an n-element vector.

Arguments

A

The n-by-m array used in the least-squares minimization.

B

The n-by-p array used in the equality constraint.

C

An m-element input vector containing the right-hand side of the least-squares system.

D

A p-element input vector containing the right-hand side of the equality constraint.

Keywords

DOUBLE

Set this keyword to use double-precision for computations and to return a double-precision (real or complex) result. Set DOUBLE = 0 to use single-precision for computations and to return a single-precision (real or complex) result. The default is /DOUBLE if A is double precision, otherwise the default is DOUBLE = 0.

RESIDUAL

Set this keyword to a named variable in which to return a scalar giving the residual sum-of-squares for Result. If n = m + p then RESIDUAL will be zero.

STATUS

Set this keyword to a named variable that will contain the status of the computation. Possible values are:

STATUS = 0: The computation was successful.
STATUS = 1: The factorization of B is singular, so rank(B) < p. No least squares solution can be computed.
STATUS = 2: The factorization of A is singular, so rank 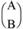< n. No least squares solution can be computed.
STATUS < 0: One of the input arguments had an illegal value.

Note: If STATUS is not specified, any error messages will output to the screen.

Version History

5.6	Introduced

Resources and References

For details see Anderson et al., LAPACK Users' Guide, 3rd ed., SIAM, 1999.