BROYDEN

The BROYDEN function solves a system of n nonlinear equations (where n ≥ 2) in n dimensions using a globally-convergent Broyden’s method.

Examples

We can use BROYDEN to solve the non-linear system of equations defined by the BROYFUNC function above:

FUNCTION broyfunc, X
   RETURN, [3.0 * X[0] - COS(X[1]*X[2]) - 0.5,$
   X[0]^2 - 81.0*(X[1] + 0.1)^2 + SIN(X[2]) + 1.06,$
   EXP(-X[0]*X[1]) + 20.0 * X[2] + (10.0*!PI - 3.0)/3.0]
END
;Provide an initial guess as the algorithm's starting point:
X = [-1.0, 1.0, 2.0]
;Compute the solution:
result = BROYDEN(X, 'BROYFUNC')
;Print the result:
PRINT, result

IDL prints:

   0.500000  -1.10731e-07  -0.523599

The exact solution (to eight-decimal accuracy) is [0.5, 0.0, -0.52359877].

Syntax

Result = BROYDEN( X, Vecfunc [, CHECK=variable] [, /DOUBLE] [, EPS=value] [, ITMAX=value] [, STEPMAX=value] [, TOLF=value] [, TOLMIN=value] [, TOLX=value] )

Return Value

This function returns an n-element vector containing the solution.

Arguments

X

An n-element vector (where n ≥ 2) containing an initial guess at the solution of the system.

If BROYDEN is complex then only the real part is used for the computation.

Vecfunc

A scalar string specifying the name of a user-supplied IDL function that defines the system of non-linear equations. This function must accept a vector argument X and return a vector result.

For example, suppose we wish to solve the following system:

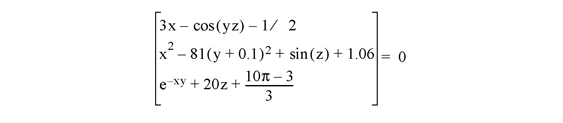
To represent this system, we define an IDL function named BROYFUNC:

FUNCTION broyfunc, X

   RETURN, [3.0 * X[0] - COS(X[1]*X[2]) - 0.5,$

   X[0]^2 - 81.0*(X[1] + 0.1)^2 + SIN(X[2]) + 1.06,$

   EXP(-X[0]*X[1]) + 20.0 * X[2] + (10.0*!PI - 3.0)/3.0]

END

Keywords

CHECK

BROYDEN calls an internal function named fmin() to determine whether the routine has converged to a local rather than a global minimum (see Numerical Recipes, section 9.7). Use the CHECK keyword to specify a named variable which will be set to 1 if the routine has converged to a local minimum or to 0 if not. If the routine does converge to a local minimum, try restarting from a different initial guess to obtain the global minimum.

DOUBLE

Set this keyword to force the computation to be done in double-precision arithmetic.

EPS

Set this keyword to a number close to machine accuracy, used to remove noise from each iteration. The default is 10^-7for single precision, and 10^-14for double precision.

ITMAX

Use this keyword to specify the maximum allowed number of iterations. The default is 200.

STEPMAX

Use this keyword to specify the scaled maximum step length allowed in line searches. The default value is 100.0.

TOLF

Set the convergence criterion on the function values. The default value is 1.0 x 10^-4.

TOLMIN

Set the criterion for deciding whether spurious convergence to a minimum of the function fmin() has occurred. The default value is 1.0 x 10^-6.

TOLX

Set the convergence criterion on X. The default value is 1.0 x 10^-7.

Version History

Pre 4.0

Introduced

Resources and References

BROYDEN is based on the routine broydn described in section 9.7 of Numerical Recipes in C: The Art of Scientific Computing (Second Edition), published by Cambridge University Press, and is used by permission.