The BANDPASS_FILTER function applies a lowpass, bandpass, or highpass filter to a one-channel image.
A bandpass filter is useful when the general location of the noise in the frequency domain is known. The bandpass filter allows frequencies within the chosen range through and attenuates frequencies outside of the given range.
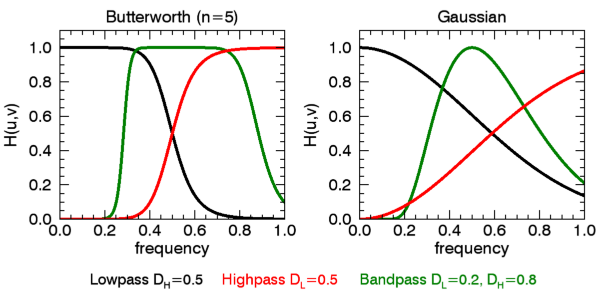
The following diagrams give a visual interpretation of the transfer functions:
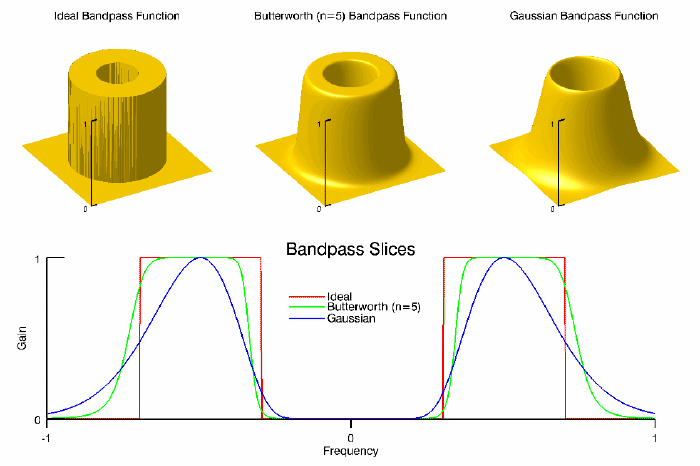
This routine is written in the IDL language. Its source code can be found in the file bandpass_filter.pro in the lib subdirectory of the IDL distribution.
Syntax
Result = BANDPASS_FILTER( ImageData, LowFreq, HighFreq [, /IDEAL] [, BUTTERWORTH=value] [, /GAUSSIAN] )
Return Value
Returns a filtered image array of the same dimensions and type as ImageData.
Arguments
ImageData
A two-dimensional array containing the pixel values of the input image.
LowFreq
The lower limit of the pass-through frequency band. This value should be between 0 and 1 (inclusive), and must be less than HighFreq.
HighFreq
The upper limit of the pass-through frequency band. This value should be between 0 and 1 (inclusive), and must be greater than LowFreq.
Keywords
IDEAL
Set this keyword to use an ideal bandpass filter. In ideal bandpass filters, frequencies within the given range are passed through without attenuation and frequencies outside of the given range are completely removed. This behavior makes ideal bandpass filters very sharp.
The centered Fast Fourier Transform (FFT) is filtered by the following function, where DL is the lower bound of the frequency band, DH is the upper bound of the frequency band, and D(u,v) is the distance between a point (u,v) in the frequency domain and the center of the frequency rectangle:
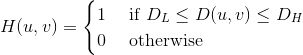
BUTTERWORTH
Set this keyword to the dimension of the Butterworth filter to apply to the frequency domain. With a Butterworth bandpass filter, frequencies at the center of the frequency band are unattenuated and frequencies at the edge of the band are attenuated by a fraction of the maximum value. The Butterworth filter does not have sharp discontinuities between frequencies that are passed and filtered.
The default for BANDPASS_FILTER is BUTTERWORTH=1.
The centered FFT is filtered by one of the following functions, where D0 is the center of the frequency band, W is the width of the frequency band, D=D(u,v) is the distance between a point (u,v) in the frequency domain and the center of the frequency rectangle, and n is the dimension of the Butterworth filter:
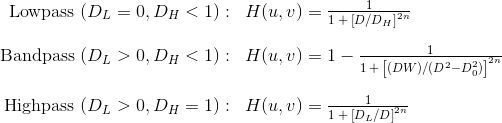
A low Butterworth dimension is close to Gaussian, and a high Butterworth dimension is close to Ideal.
GAUSSIAN
Set this keyword to use a Gaussian bandpass filter. In this type of filter, the transition between unfiltered and filtered frequencies is very smooth.
The centered FFT is filtered by one of the following functions, where D0 is the center of the frequency band, W is the width of the frequency band, and D=D(u,v) is the distance between a point (u,v) in the frequency domain and the center of the frequency rectangle:
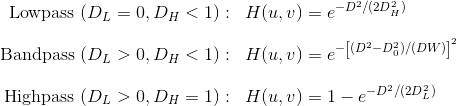
Examples
Here, we plot the frequency response of the Butterworth (n=5) and Gaussian filters. For the lowpass filter we use a high-frequency cutoff of 0.5, for highpass we use a cutoff of 0.5, and for the bandpass we use DL=0.2 and DH=0.8.
m = [0.2,0.27,0.05,0.1]
p = PLOT('1/(1 + (X/0.5)^10)', '3', DIM=[600,300], FONT_SIZE=10, $
XRANGE=[0,1], YRANGE=[0,1.1], LAYOUT=[2,1,1], MARGIN=m, $
XTITLE='frequency', YTITLE='H(u,v)', TITLE='Butterworth (n=5)')
p = PLOT('1-1/(1 + (X*0.6/(X^2-0.5^2))^10)', '3g', /OVERPLOT)
p = PLOT('1/(1 + (0.5/X)^10)', '3r', /OVERPLOT)
p = PLOT('exp(-X^2/(2*0.5^2))', '3', DIM=[600,300], FONT_SIZE=10, $
XRANGE=[0,1], YRANGE=[0,1.1], LAYOUT=[2,1,2], MARGIN=m, $
XTITLE='frequency', YTITLE='H(u,v)', TITLE='Gaussian', /CURRENT)
p = PLOT('exp(-((X^2-0.5^2)/(X*0.6))^2)', '3g', /OVERPLOT)
p = PLOT('1-exp(-X^2/(2*0.5^2))', '3r', /OVERPLOT)
t = TEXT(0.15,0.05,'Lowpass $D_H=0.5$',/NORM, FONT_SIZE=9)
t = TEXT(0.37,0.05,'Highpass $D_L=0.5$',COLOR='red',/NORM, FONT_SIZE=9)
t = TEXT(0.6,0.05,'Bandpass $D_L=0.2, D_H=0.8$',COLOR='green',/NORM, FONT_SIZE=9)
p.Save, 'bandpass_filter.png', resolution=120
In the following example, we add some sinusoidal noise to an image and filter it with BANDPASS_FILTER, using the BUTTERWORTH keyword.
file = FILEPATH('moon_landing.png', SUBDIR=['examples','data'])
imageOriginal = READ_PNG(file)
xCoords = LINDGEN(300,300) MOD 300
yCoords = TRANSPOSE(xCoords)
noise = -SIN(xCoords*2)-SIN(yCoords*2)
imageNoise = imageOriginal + 50*noise
imageFiltered = BANDPASS_FILTER(imageNoise, 0, 0.4, $
BUTTERWORTH=20)
i=IMAGE(imageOriginal, LAYOUT=[3,1,1], TITLE='Original Image', $
DIMENSIONS=[700,300])
i=IMAGE(imageNoise, LAYOUT=[3,1,2], /CURRENT, TITLE='Added Noise')
i=IMAGE(imageFiltered, LAYOUT=[3,1,3], /CURRENT, $
TITLE='Butterworth Filtered')
i.Save, 'bandpass_filter_butterworth_ex.gif', resolution=120

Reference
Gonzalez, R.C., and R.E. Woods. Digital Image Processing, 3rd edition. Pearson Education, Upper Saddle River, New Jersey, 2008.
Version History
|
7.1 |
Introduced |
|
8.5.2 |
Add equations for lowpass and highpass filters.
|
See Also
MEAN_FILTER, ESTIMATOR_FILTER, BANDREJECT_FILTER, WIENER_FILTER, LEAST_SQUARES_FILTER