An activation function is a mathematical tool used in machine learning to impart non-linearities into linear systems. Choosing the proper activation function(s) is an important step in designing your neural network. The IDLmlafISRLU (inverse square root linear unit) activation function is implemented with the following formula:
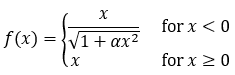
Example
Compile_opt idl2
Data = [-2.0, -1.0, 0.0, 1.0, 2.0]
actFunc = IDLmlafISRLU(1.0)
Print, actFunc(data)
Syntax
actFunc = IDLmlafISRLU(Alpha)
Result = actFunc(X [, GRADIENT=value])
Note: IDL activation functions work by overloading the function operator. To avoid compilation problems, make sure that every routine that uses an activation function contains the statement:
Compile_opt idl2
Arguments
Alpha
Specify a number that will serve as alpha coefficient for the activation function (see the formula).
Keywords
GRADIENT (optional)
Set this keyword to a named variable to receive the gradient of the activation function at each point in the input X array. The output gradient will have the same dimensions as the input X array.
Version History
See Also
IDLmlafArcTan, IDLmlafBentIdentity, IDLmlafBinaryStep, IDLmlafELU, IDLmlafGaussian, IDLmlafIdentity, IDLmlafISRU, IDLmlafLogistic, IDLmlafPReLU, IDLmlafReLU, IDLmlafSinc, IDLmlafSinusoid, IDLmlafSoftExponential, IDLmlafSoftmax, IDLmlafSoftPlus, IDLmlafSoftSign, IDLmlafTanH