SIMPLEX

The SIMPLEX function uses the simplex method to solve linear programming problems. Given a set of N independent variables X_i, where i = 0, ..., N, the simplex method seeks to maximize the following function,

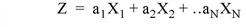
with the assumption that X_i≥ 0. The X_i are further constrained by the following equations:

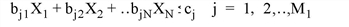
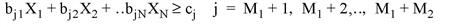
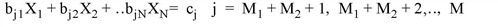
where M = M₁ + M₂ + M₃ is the total number of equations, and the constraint values c_jmust all be positive.

To solve the above problem using the SIMPLEX function, the Z equation is rewritten as a vector:

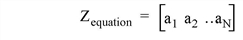
The constraint equations are rewritten as a matrix with N+1 columns and M rows, where all of the b coefficients have had their sign reversed:

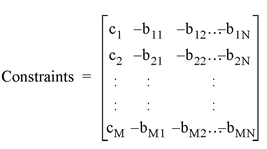
Note: The constraint matrix must be organized so that the coefficients for the less-than (<) equations come first, followed by the coefficients of the greater-than (>) equations, and then the coefficients of the equal (=) equations.

The SIMPLEX function is based on the routine simplx described in section 10.8 of Numerical Recipes in C: The Art of Scientific Computing (Second Edition), published by Cambridge University Press, and is used by permission.

Syntax

Result = SIMPLEX( Zequation, Constraints, M₁, M₂, M₃ [, Tableau [, Izrov [, Iposv] ] ] [, /DOUBLE] [, EPS = value] [, STATUS = variable] )

Return Value

The Result is a vector of N+1 elements containing the maximum Z value and the values of the N independent X variables (the optimal feasible vector):

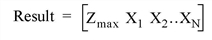
Arguments

Zequation

A vector containing the N coefficients of the Z_equation to be maximized.

Constraints

An array of N+1 columns by M rows containing the constraint values and coefficients for the constraint equations.

M1

An integer giving the number of less-than constraint equations contained in Constraints. M1 may be zero, indicating that there are no less than constraints.

M2

An integer giving the number of greater-than constraint equations contained in Constraints. M2 may be zero, indicating that there are no greater than constraints.

M3

An integer giving the number of equal-to constraint equations contained in Constraints. M3 may be zero, indicating that there are no equal to constraints. The total of M1 + M2 + M3 should equal M, the number of constraint equations.

Tableau

Set this optional argument to a named variable in which to return the output array from the simplex algorithm. For more detailed discussion about this argument, see the write-up in section 10.8 of Numerical Recipes in C.

Izrov

Set this optional argument to a named variable in which to return the output izrov variable from the simplex algorithm. For more detailed discussion about this argument, see the write-up in section 10.8 of Numerical Recipes in C.

Iposv

Set this optional argument to a named variable in which to return the output iposv variable from the simplex algorithm. For more detailed discussion about this argument, see the write-up in section 10.8 of Numerical Recipes in C.

Keywords

DOUBLE

Set this keyword to use double-precision for computations and to return a double-precision result. Set DOUBLE to 0 to use single-precision for computations and to return a single-precision result. The default is /DOUBLE if any of the inputs are double-precision, otherwise the default is 0.

EPS

Set this keyword to a number close to machine accuracy, which is used to test for convergence at each iteration. The default is 10^–6.

STATUS

Set this keyword to a named variable to receive the status of the operation. Possible status values are:

Value	Description
0	Successful completion.
1	The objective function is unbounded.
2	No solution satisfies the given constraints.
3	The routine did not converge.

Examples

The following example is taken from Numerical Recipes in C.

Find the Z value which maximizes the equation Z = X₁ + X₂ + 3 X₃ - 0.5 X₄, with the following constraints:

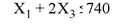
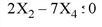
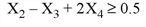
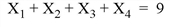
To find the solution, enter the following code at the IDL command line:

; Set up the Zequation with the X coefficients.
Zequation = [1,1,3,-0.5]
; Set up the Constraints matrix.
Constraints = [ $
   [740, -1,  0, -2,  0], $
   [  0,  0, -2,  0,  7], $
   [0.5,  0, -1,  1, -2], $
   [  9, -1, -1, -1, -1] ]
; Number of less-than constraint equations.
m1 = 2 
; Number of greater-than constraint equations.
m2 = 1 
; Number of equal constraint equations.
m3 = 1 
; 
; Call the function.
result = SIMPLEX(Zequation, Constraints, m1, m2, m3)
;
; Print out the results.
PRINT, 'Maximum Z value is: ', result[0]
PRINT, 'X coefficients are: '
PRINT, result[1:*]

IDL prints:

Maximum Z value is:       17.0250

X coefficients are:

      0.000000      3.32500      4.72500     0.950000

Therefore, the optimal feasible vector is X₁ = 0.0, X₂ = 3.325, X₃ = 4.725, and X₄ = 0.95.

Version History

5.5	Introduced