LEAST_SQUARES

LEAST_SQUARES_FILTER

The LEAST_SQUARES_FILTER function reduces degradation and noise in an image based on the mean and variance of the degradation and noise. This is also known as a constrained least squares filter.

If the degraded image is modeled in the spatial domain by

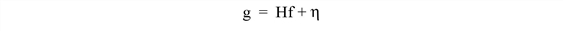
the constrained least squares filter seeks to find the minimum of

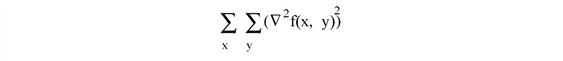
subject to the constraint

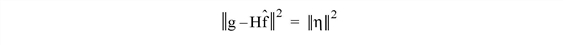
The solution to this problem is given by the following equation:

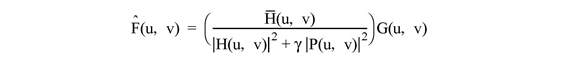
where H(u,v) is the degradation function and

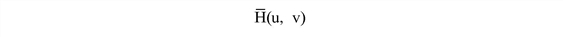
is the complex conjugate of the degradation function. P(u,v) is the Laplacian operator frequency domain, and γ is a parameter which is set to meet the previously-mentioned constraint. G(u,v) is the frequency domain of the observed image, and

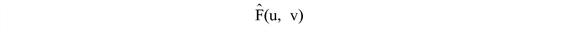
is the frequency domain estimate of the undegraded image.

This routine is written in the IDL language. Its source code can be found in the file least_squares_filter.pro in the lib subdirectory of the IDL distribution.

Examples

In the following example, we introduce some degradation to an image and then filter it with LEAST_SQUARES_FILTER.

; Read an image.

file = FILEPATH('moon_landing.png', SUBDIR=['examples','data'])

astronaut = READ_PNG_png(file)

image_size = SIZE(astronaut, /DIMENSIONS)

; Blur the image with a known degradation transfer function.

x_coords = LINDGEN(image_size) mod image_size[0] - image_size[0]/2 + 1

y_coords = TRANSPOSE(x_coords)

k = 0.0025

degradation = EXP(-k * (x_coords^2 + y_coords^2 ) ^ (5d/6d) )

blurred = degradation*FFT(astronaut, /CENTER)

blurred = REAL_PART(FFT(blurred, /INVERSE, /CENTER))

; Filter the degraded image with the least squares filter.

filtered = LEAST_SQUARES_FILTER(blurred, degradation, 10d^(-18.22))

; Display the original, blurred, and filtered images.

g0 = IMAGE(astronaut, LAYOUT=[3,1,1], DIMENSIONS=[3,1]*image_size, $

   TITLE='Original image')

g1 = IMAGE(blurred, LAYOUT=[3,1,2], /CURRENT, $

   TITLE='Blurred')

g2 = IMAGE(filtered, LAYOUT=[3,1,3], /CURRENT, $

   TITLE='Filtered with LEAST_SQUARES_FILTER')

Syntax

Result = LEAST_SQUARES_FILTER( ImageData, DegradationFunction, Gamma )

Return Value

Returns a double-precision floating-point array of the same dimensions as ImageData.

Arguments

ImageData

A two-dimensional array containing the pixel values of the input image.

DegradationFunction

A two-dimensional array representing the transfer function that describes the image degradation.

Degraded images are modeled as the product of the true image with a degradation function and the addition of noise, represented by G(u,v) = H(u,v)F(u,v) + N(u,v). G(u,v) is the observed image in the frequency domain, H(u,v) is the degradation function, F(u,v) is the true image in the frequency domain, and N(u,v) is the noise function in the frequency domain.

Gamma

A scalar with a value chosen to meet the constrained least squares criterion.

Keywords

None

Version History

7.1	Introduced