LEGENDRE

The LEGENDRE function returns the value of the associated Legendre polynomial 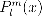, where l is the degree and m is the order. LEGENDRE can also be used to compute the Legendre polynomial when m=0 is specified.

The associated Legendre functions are solutions of the general Legendre equation:

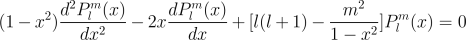
with orthogonality constraint for fixed m:

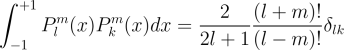
The Legendre polynomials are the solutions to the Legendre equation with order m = 0. For positive m, the associated Legendre functions can be written in terms of the Legendre polynomials of degree l as:

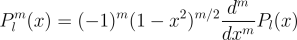
Associated polynomials for negative m are related to positive m by:

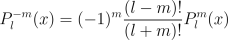
LEGENDRE is based on the routine plgndr described in section 6.8 of Numerical Recipes in C: The Art of Scientific Computing (Second Edition), published by Cambridge University Press, and is used by permission.

Examples

Compute the value of the Legendre polynomial of degree L=2:

IDL> x = [-0.75, -0.5, -0.25, 0.25, 0.5, 0.75]

IDL> result = LEGENDRE(X, 2)

IDL> result

        0.34375000     -0.12500000     -0.40625000     -0.40625000     -0.12500000      0.34375000

Compute the value of the associated Legendre polynomial at the same X values for degree L=2 and order M=1:

IDL> result = LEGENDRE(X, 2, 1)

IDL> result

         1.4882351       1.2990381      0.72618437     -0.72618437      -1.2990381      -1.4882351

Syntax

Result = LEGENDRE( X, L [, M] [, /DOUBLE] )

Return Value

If all arguments are scalar, the function returns a scalar. If all arguments are arrays, the function matches up the corresponding elements of X, L, and M, returning an array with the same dimensions as the smallest array. If one argument is a scalar and the other arguments are arrays, the function uses the scalar value with each element of the arrays, and returns an array with the same dimensions as the smallest input array.

If any of the arguments are double-precision or if the DOUBLE keyword is set, the result is double-precision, otherwise the result is single-precision.

Arguments

X

The expression for which is evaluated. Values for X must be in the range –1 ≤X ≤ 1.

L

An integer scalar or array, L≥ 0, specifying the degree l . If L is of type float, it will be truncated to an integer.

M

An integer scalar or array, –L≤M≤L, specifying the order m. If M is not specified, then M = 0 is used and the Legendre polynomial, P_l(x), is returned. If M is of type float, it will be truncated to an integer.

Keywords

DOUBLE

Set this keyword to force the computation to be done in double-precision arithmetic.

Version History

5.4	Introduced