LAGUERRE

The LAGUERRE function returns the value of the associated Laguerre polynomial 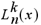. The associated Laguerre polynomials are solutions to the differential equation:

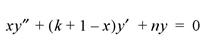
with orthogonality constraint:

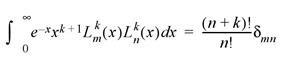
Laguerre polynomials are used in quantum mechanics, for example, where the wave function for the hydrogen atom is given by the Laguerre differential equation.

This routine is written in the IDL language. Its source code can be found in the file laguerre.pro in the lib subdirectory of the IDL distribution.

Examples

To compute the value of the Laguerre polynomial at the following X values:

;Define the parametric X values:

X = [0.0, 0.2, 0.4, 0.6, 0.8, 1.0]

;Compute the Laguerre polynomial of order N=2, K=1:

result = LAGUERRE(X, 2, 1)

;Print the result:

PRINT, result

IDL prints:

3.00000   2.42000   1.88000   1.38000   0.920000   0.500000

This is the exact solution vector to six-decimal accuracy.

Syntax

Result = LAGUERRE( X, N [, K] [, COEFFICIENTS=variable] [, /DOUBLE] )

Return Value

This function returns a scalar or array with the same dimensions as X. If X is double-precision or if the DOUBLE keyword is set, the result is double-precision complex, otherwise the result is single-precision complex.

Arguments

X

The value(s) at which 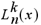is evaluated. X can be either a scalar or an array.

N

A scalar integer, N ≥ 0, specifying the order n of 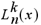. If N is of type float, it will be truncated.

K

A scalar, K ≥ 0, specifying the order k of 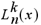. If K is not specified, the default K = 0 is used and the Laguerre polynomial, L_n(x), is returned.

Keywords

COEFFICIENTS

Set this keyword to a named variable that will contain the polynomial coefficients in the expansion C[0] + C[1]x + C[2]x² + ... .

DOUBLE

Set this keyword to force the computation to be done in double-precision arithmetic.

Version History

5.4	Introduced