POWELL

The POWELL procedure minimizes a user-written function Func of two or more independent variables using the Powell method. POWELL does not require a user-supplied analytic gradient.

POWELL is based on the routine powell described in section 10.5 of Numerical Recipes in C: The Art of Scientific Computing (Second Edition), published by Cambridge University Press, and is used by permission.

Examples

We can use POWELL to minimize the function POWFUNC given above.

FUNCTION powfunc, X
   RETURN, (X[0] + 2.0*X[1]) * EXP(-X[0]^2 -X[1]^2)
END
PRO TEST_POWELL
   ; Define the fractional tolerance:
   ftol = 1.0e-4
   ; Define the starting point:
   P = [.5d, -.25d]
   ; Define the starting directional vectors in column format:
   xi = TRANSPOSE([[1.0, 0.0],[0.0, 1.0]])
   ; Minimize the function:
   POWELL, P, xi, ftol, fmin, 'powfunc'
   ; Print the solution point:
   PRINT, 'Solution point: ', P
   ; Print the value at the solution point:
   PRINT, 'Value at solution point: ', fmin
END
TEST_POWELL

IDL prints:

Solution point:    -0.31622777     -0.63245552

Value at solution point:    -0.95900918

The exact solution point is [-0.31622777, -0.63245553].

The exact minimum function value is -0.95900918.

Syntax

POWELL, P, Xi, Ftol, Fmin, Func [, /DOUBLE] [, ITER=variable] [, ITMAX=value]

Arguments

P

On input, P is an n-element vector specifying the starting point. On output, it is replaced with the location of the minimum.

Note: If POWELL is complex then only the real part is used for the computation.

Xi

On input, Xi is an initial n by n element array whose columns contain the initial set of directions (usually the n unit vectors). On output, it is replaced with the then-current directions.

Ftol

An input value specifying the fractional tolerance in the function value. Failure to decrease by more than Ftol in one iteration signals completeness. For single-precision computations, a value of 1.0 x 10^-4 is recommended; for double-precision computations, a value of 1.0 x 10^-8 is recommended.

Fmin

On output, Fmin contains the value at the minimum-point P of the user-supplied function specified by Func.

Func

A scalar string specifying the name of a user-supplied IDL function of two or more independent variables to be minimized. This function must accept a vector argument X and return a scalar result.

For example, suppose we wish to minimize the function

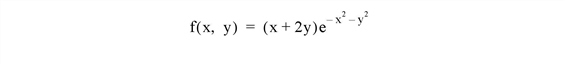
To evaluate this expression, we define an IDL function named POWFUNC:

FUNCTION powfunc, X

   RETURN, (X[0] + 2.0*X[1]) * EXP(-X[0]^2 -X[1]^2)

END

Keywords

DOUBLE

Set this keyword to force the computation to be done in double-precision arithmetic.

ITER

Use this keyword to specify an output variable that will be set to the number of iterations performed.

ITMAX

Use this keyword to specify the maximum allowed number of iterations. The default is 200.

Note: POWELL halts once the value specified with ITMAX has been reached.

Version History

4.0	Introduced