The REBIN function resizes a vector or array to dimensions given by the parameters Di. The supplied dimensions must be integral multiples or factors of the original dimension. The expansion or compression of each dimension is independent of the others, so that each dimension can be expanded or compressed by a different value.

If the dimensions of the desired result are not integer multiples of the original dimensions, use the CONGRID function.

Examples

Create and display a simple image by entering:

D = SIN(DIST(50)/4)
im = IMAGE(D)

Resize the image to be 5 times its original size and display the result by entering:

D = REBIN(D, 250, 250)
im = IMAGE(D)
 

Display an image array in the original size, then use REBIN to enlarge it:

; Select the file.
file = FILEPATH('convec.dat', SUBDIRECTORY = ['examples', 'data'])
 
; Use READ_BINARY to read in the data,
; specifying known data dimensions.
convec_image = READ_BINARY(file, DATA_DIMS = [248, 248])
 
; Use the IMAGE function to display
; the original image with a color table.
im = IMAGE(convec_image, RGB_TABLE=28)
 
; Use the REBIN function to increase the
; image array size to three times the original size
rebinIm = REBIN(convec_image, 744, 744)
 
; Display the resized image in a new window with a color table.
im2 = IMAGE(rebinIm, RGB_TABLE=28)

Syntax

Result = REBIN( Array, D1[, ..., D8] [, /SAMPLE] )

Return Value

Returns the resized array or vector of the specified dimensions.

Arguments

Array

The array to be resampled. Array can be of any basic type except complex or string.

Di

Either an array or a series of scalar expressions specifying the dimensions of the result. If a single argument is specified, it can be either a scalar expression or an array of up to eight elements. If multiple arguments are specified, they must all be scalar expressions. Up to eight dimensions can be specified.

Note: The dimensions of the resulting resampled array must be integer multiples or factors of the corresponding original dimensions.

Keywords

SAMPLE

Normally, REBIN uses bilinear interpolation when magnifying and neighborhood averaging when minifying. Set the SAMPLE keyword to use nearest neighbor sampling for both magnification and minification. Bilinear interpolation gives higher quality results but requires more time.

Rules Used by REBIN

Assume the original vector X has n elements and the result is to have m elements.

Let f = n/m, the ratio of the size of the original vector, X to the size of the result. 1/f must be an integer if n < m (expansion). f must be an integer if compressing, (n > m). The various resizing options can be described as:

  • Expansion, n < m, SAMPLE = 0: Yi = F(X, f •i)       i = 0, 1, ... , m-1

The linear interpolation function, F(X, p) that interpolates X at location p, is defined as:

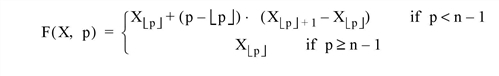
  • Expansion, n < m, SAMPLE = 1:

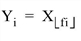
  • Compression, n > m, SAMPLE = 0:

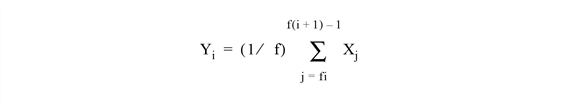
  • Compression, n > m, SAMPLE = 1:

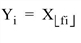
  • No change, n = m: Yi = Xi

Endpoint Effects When Expanding

When expanding an array, REBIN interpolates, it never extrapolates. Each of the n-1 intervals in the n-element input array produces m/n interpolates in the m-element output array. The last m/n points of the result are obtained by duplicating element n-1 of the input array because their interpolates would lie outside the input array.

For example

; A four point vector:
A = [0, 10, 20, 30]
; Expand by a factor of 3:
B = REBIN(A, 12)
PRINT, B

IDL prints:

0 3 6 10 13 16 20 23 26 30 30 30

Note that the last element is repeated three times. If this effect is undesirable, use the INTERPOLATE function. For example, to produce 12 equally spaced interpolates from the interval 0 to 30:

B = INTERPOLATE(A, 3./11. * FINDGEN(12))
PRINT, B

IDL prints:

0 2 5 8 10 13 16 19 21 24 27 30

Here, the sampling ratio is (n - 1)/(m - 1).

Version History

Original

Introduced

See Also

CONGRID