The MEAN_FILTER function applies mean filter noise reduction on a one-channel image or a multi-channel (True Color) image.
For each pixel in the image, the mean filter analyzes the neighboring pixels. The mean is computed for this neighborhood and the pixel is replaced with the mean value.
This routine is written in the IDL language. Its source code can be found in the file mean_filter.pro in the lib subdirectory of the IDL distribution.
Syntax
Result = MEAN_FILTER( ImageData, Width [, Height] [, /ARITHMETIC] [, /GEOMETRIC] [, /IGNORE_INVALID] [, INVALID=value] [, MISSING=value] [, /NAN] [, /TRUE={1|2|3}])
Return Value
Returns an array containing the filtered image, which has the same dimensions and type as ImageData.
Arguments
ImageData
A two- or three-dimensional array containing the pixel values of the input image.
Width
The width of the two-dimensional neighborhood. Since the neighborhood is centered on a pixel, this value must be an odd, positive integer.
Height
The height of the two-dimensional neighborhood. Since the neighborhood is centered on a pixel, this value must be an odd, positive integer. If this value is omitted, Height is set to Width, resulting in a square neighborhood.
Keywords
ARITHMETIC
Set this keyword to replace a pixel with the neighborhood arithmetic mean. Using the arithmetic mean smooths local variations in the data and reduces blurry noise.
If neither the ARITHMETIC nor GEOMETRIC keywords are specified, ARITHMETIC will be used as the default computation.
If Sx,y represents the M x N neighborhood surrounding the pixel ƒ(x,y), then the arithmetically-filtered mean pixel is given by:
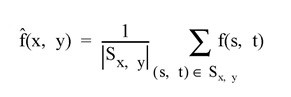
GEOMETRIC
Set this keyword to replace a pixel with the neighborhood geometric mean. Using the geometric mean smooths and reduces noise in much the same way as the arithmetic mean filter, but retains more original detail. Achieving this improved performance comes at the cost of increased processing time.
If Sx,y represents the M x N neighborhood surrounding the pixel ƒ(x,y), then the geometrically-filtered mean pixel is given by:
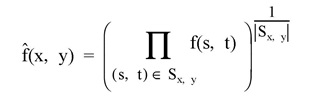
IGNORE_INVALID
By default, if the INVALID keyword is set, then missing data points are still included in the computation but are treated as having the value zero. Instead, if IGNORE_INVALID is set, then missing data points will be completely ignored during the computation. This has the advantage of not "polluting" the good data with zero values, but will introduce bias because there will be fewer points within a neighborhood that contains missing data.
INVALID
Set this keyword to a scalar value of the same type as ImageData that should be used to indicate missing or invalid data within ImageData. Missing data are set to zero when computing the mean of an element’s neighborhood (you can set the IGNORE_INVALID keyword to change this behavior). In Result, missing elements are replaced by the mean of all other valid points within that element’s neighborhood.
Tip: The INVALID keyword has the same effect as the NAN keyword, but is useful for byte or integer data which have missing values.
Note: The INVALID keyword uses a simple comparison to ignore values and should not be set to NaN. For floating-point data, you can use the INVALID and NAN keywords simultaneously to filter out both user-defined values and NaN or Infinity values.
MISSING
Set this keyword to the value that will be substituted for locations in the result where all of the neighborhood's data is invalid. This keyword is used only if the INVALID or NAN keyword is set. The default is 0 for byte or integer data, and NaN for floating-point data.
NAN
Set this keyword to check for occurrences of the IEEE floating-point values NaN or Infinity in the input data. Pixels with the value NaN or Infinity are treated as missing data. Missing data are ignored when computing the mean of an element’s neighborhood. In Result, missing elements are replaced by the mean of all other valid points within that element’s neighborhood.
Note: MEAN_FILTER should never be called without the NAN keyword if the input array may possibly contain NaN or Infinity values.
TRUE
If ImageData is a three-dimensional array (a multichannel image), set this keyword to 1, 2, or 3 to indicate which dimension represents the channels. The default is 1, for pixel interleaving, (3, m, n). A value of 2 indicates line interleaving (m, 3, n), and 3 indicates band interleaving, (m, n, 3).
Examples
Example 1
In the following example, we add some binomial noise to an image, and filter it with MEAN_FILTER.
file = FILEPATH('moon_landing.png', SUBDIR=['examples','data'])
imageOriginal = READ_PNG(file)
noise = RANDOMN(SYSTIME(/SECONDS), 300, 300, $
BINOMIAL=[10,.5])*30-150
imageNoise = imageOriginal + noise < 255 > 0
imageMean = MEAN_FILTER(imageNoise, 3)
imageGeo = MEAN_FILTER(imageNoise, 3, /GEOMETRIC)
i = image(imageOriginal, layout=[2,2,1], title='Original', margin=0.1)
i = image(imageNoise, layout=[2,2,2], title='With Noise', margin=0.1, /current)
i = image(imageMean, layout=[2,2,3], title='Mean_Filter', margin=0.1, /current)
i = image(imageGeo, layout=[2,2,4], title='Mean_Filter Geometric', margin=0.1, /current)

Version History
|
7.1 |
Introduced |
| 8.9 |
Added IGNORE_INVALID
|
See Also
ESTIMATOR_FILTER, BANDPASS_FILTER, BANDREJECT_FILTER, WIENER_FILTER, LEAST_SQUARES_FILTER