Points in xyz space are expressed by vectors of homogeneous coordinates. These vectors are translated, rotated, scaled, and projected onto the two-dimensional drawing surface by multiplying them by transformation matrices. The geometric transformations used by IDL are taken from Chapters 7 and 8 of Foley and Van Dam (Foley, J.D., and A. Van Dam (1982), Fundamentals of Interactive Computer Graphics, Addison-Wesley Publishing Co.). Consult this book for a detailed description of homogeneous coordinates and transformation matrices since this topic is an overview.
Homogeneous Coordinates
A point in homogeneous coordinates is represented as a four-element column vector of three coordinates and a scale factor w ¹¹¹ 0. For example:
P(wx, wy, wz, w) º P(x/w, y/w, z/w, 1) º (x, y, z)
One advantage of this approach is that translation, which normally must be expressed as an addition, can be represented as a matrix multiplication. Another advantage is that homogeneous coordinate representations simplify perspective transformations. The notion of rows and columns used by IDL is opposite that of Foley and Van Dam (1982). In IDL, the column subscript is first, while in Foley and Van Dam (1982) the row subscript is first. This changes all row vectors to column vectors and transposes matrices.
Right-Handed Coordinate System
The coordinate system is right-handed so that when looking from a positive axis to the origin, a positive rotation is counterclockwise. As usual, the x-axis runs across the display, the y-axis is vertical, and the positive z-axis extends out from the display to the viewer. For example, a 90-degree positive rotation about the z-axis transforms the x-axis to the y-axis.
Transformation Matrices
Transformation matrices, which post-multiply a point vector to produce a new point vector, must be (4, 4). A series of transformation matrices can be concatenated into a single matrix by multiplication. If A1, A2, and A3 are transformation matrices to be applied in order, and the matrix A is the product of the three matrices, the following applies.
((P · A1) · A2) · A3 º P · ((A1 · A2) · A3) = P · A
In Object Graphics, IDL the model object that contains the displayed object stores the transformation matrix. In Direct Graphics, IDL stores the concatenated transformation matrix in the system variable field !P.T.
Note: When displaying objects in a three-dimensional view, you can precisely configure the object position using transformation matrices. See Translating, Rotating and Scaling Objects for details.
Note: For most Direct Graphic applications, it is not necessary to create, manipulate, or to even understand transformation matrices. See the T3D procedure, which implements most of the common transformations.
Each of the operations of translation, scaling, rotation, and shearing can be represented by a transformation matrix.
Translation
The transformation matrix to translate a point by (Dx, Dy, Dz) is shown below.
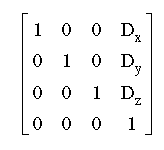
Scaling
Scaling by factors of Sx, Sy, and Sz about the x-, y-, and z-axes respectively, is represented by the matrix below.
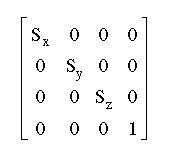
Rotation
Rotation about the x-, y-, and z-axes is represented respectively by the following three matrices:
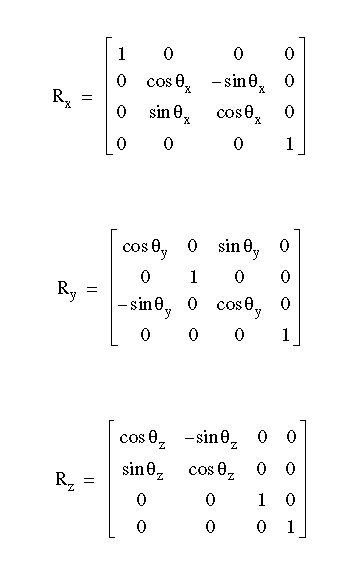
See Also
IDLgrModel, Translating, Rotating, and Scaling Objects