The Fast Fourier Transform (FFT) is used to transform an image from the spatial domain to the frequency domain, most commonly to reduce background noise from the image. The following example shows how to remove background noise from an image of the M-51 whirlpool galaxy, using the following steps:
- Perform a forward FFT to transform the image to the frequency domain
- Compute a power spectrum and determine threshold to filter out noise
- Apply a mask to the FFT-transformed image
- Perform an inverse FFT to transform the image back to the spatial domain
See Fast Fourier Transform (FFT) Background for a more complete description of this process.
The example data is available in the examples/data directory of your IDL installation. The code shown below creates the following images, each displayed in separate windows. Below is the original image of M-51 galaxy (left) and inverse-FFT-transformed image (right). The red background pixels have been reduced in the second image.


Intermediate results:
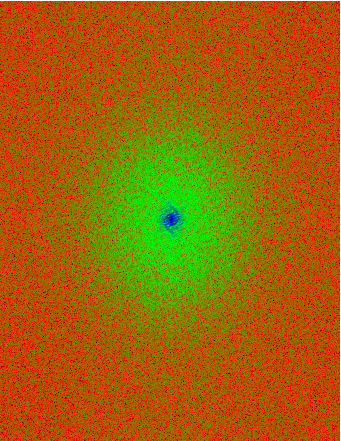
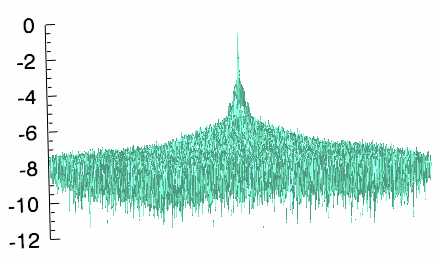
Power spectrum image (left) and surface plot (right).
imageSize = [340, 440]
file = FILEPATH('m51.dat', $
SUBDIRECTORY = ['examples', 'data'])
binary_img = READ_BINARY(file, DATA_DIMS = imageSize)
img01 = image(binary_img, RGB_TABLE = 6)
ffTransform = FFT(binary_img, /CENTER)
powerSpectrum = ABS(ffTransform)^2
scaledPowerSpect = ALOG10(powerSpectrum)
img02 = IMAGE(scaledPowerSpect, RGB_TABLE = 6)
scaledPS0 = scaledPowerSpect - MAX(scaledPowerSpect)
s3 = SURFACE(scaledPS0, $
AXIS_STYLE = 0, $
ZTITLE = 'Max-Scaled(Log(Squared Amplitude))', $
FONT_SIZE = 8, $
COLOR = 'aquamarine')
ax = AXIS('Z', LOCATION = [0, imageSize[1], 0])
mask = REAL_PART(scaledPS0) GT -7
maskedTransform = ffTransform*mask
inverseTransform = REAL_PART(FFT(maskedTransform, $
/INVERSE, /CENTER))
img03 = IMAGE(inverseTransform, RGB_TABLE = 6)
Resources