Computer hardware does not directly support the concept of multidimensional arrays. Computer memory is unidimensional, providing memory addresses that start at zero and increase serially to the highest available location. Multidimensional arrays are therefore a software concept: software (IDL in this case) maps the elements of a multi-dimensional array into a contiguous linear span of memory addresses. There are two ways that such an array can be represented in one-dimensional linear memory. These two options, which are explained below, are commonly called row major and column major. All programming languages that support multidimensional arrays must choose one of these two possibilities. This choice is a fundamental property of the language, and it affects how programs written in different languages share data with each other.

Before describing the meaning of these terms and IDL’s relationship to them, it is necessary to understand the conventions used when referring to the dimensions of an array. For mnemonic reasons, people find it useful to associate higher level meanings with the dimensions of multi-dimensional data. For example, a 2-D variable containing measurements of ozone concentration on a uniform grid covering the earth might associate latitude with the first dimension, and longitude with the second dimension. Such associations help people understand and reason about their data, but they are not fundamental properties of the language itself. It is important to realize that no matter what meaning you attach to the dimensions of an array, IDL is only aware of the number of dimensions and their size, and does not work directly in terms of these higher order concepts. Another way of saying this is that arr[d1, d2] addresses the same element of variable arr no matter what meaning you associate with the two dimensions.

In the IDL world, there are two such conventions that are widely used:

• In image processing, the first dimension of an image array is the column, and the second dimension is the row. IDL is widely used for image processing, and has deep roots in this area. Hence, the dominant convention in IDL documentation is to refer to the first dimension of an array as the column and the second dimension as the row.
• In the standard mathematical notation used for linear algebra, the first dimension of an array (or matrix) is the row, and the second dimension is the column. Note that this is the exact opposite of the image processing convention.

In computer science, the way array elements are mapped to memory is always defined using the mathematical [row, column] notation. Much of the following discussion utilizes the m x n array shown in the following figure, with m rows and n columns:

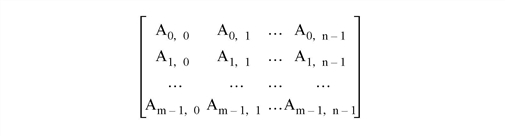
Given such a 2-dimensional matrix, there are two ways that such an array can be represented in 1-dimensional linear memory, either row by row (row major), or column by column (column major):

• Contiguous First Dimension (Column Major): In this approach, all elements of the first dimension (m in this case) are stored contiguously in memory. The 1-D linear address of element A_{d1, d2} is therefore given by the formula (d2*m + d1). As you move linearly through the memory of such an array, the first (leftmost) dimension changes the fastest, with the second dimension (n, in this case) incrementing every time you come to the end of the first dimension:

A_0,0,  A_1,0,  …,  A_m-1,0,  A_0,1,  A_1,1,  …,  A_m-1,1,  …

Computer languages that map multidimensional arrays in this manner are called column major, following the mathematical [row, column] notation. IDL and Fortran are both examples of column-major languages.

• Contiguous Second Dimension (Row Major): In this approach, all elements of the second dimension (n, in this case) are stored contiguously in memory. The 1-D linear address of element A_{d1, d2} is therefore given by the formula (d1*n + d2). As you move linearly through the memory of such an array, the second dimension changes the fastest, with the first dimension (m in this case) incrementing every time you come to the end of the second dimension:

A_0,0,  A_0,1,  …,  A_0,n-1, A_1,0,  A_1,1,  …,  A_1,n-1,  …

Computer languages that map multidimensional arrays in this manner are known as row major. Examples of row-major languages include C and C++.

The terms row major and column major are widely used to categorize programming languages. It is important to understand that when programming languages are discussed in this way, the mathematical convention is used (the first dimension represents the row and the second dimension represents the column). If you use the image-processing convention (in which the first dimension represents the column and the second dimension represents the row), you should be careful to make note of the distinction.

Note: IDL users who are comfortable with the IDL image-processing-oriented array notation [column, row] frequently follow the reasoning outlined above and incorrectly conclude that IDL is a row-major language. The often-overlooked cause of this mistake is that the standard definition of the terms row major and column major assume the mathematical [row, column] notation. In such cases, it can be helpful to look beyond the row/column terminology and think in terms of which dimension is contiguous in memory.

Note that the m x n array shown above could be represented with equal accuracy as having m columns and n rows, as shown in the figure below. This corresponds to the image-processing [column, row] notation. It is important to note that while the representation shown is the transpose of the representation in the figure above, the data stored in the computer memory are identical. Only the two-dimensional representation, which takes its form from the notational convention used, has changed. The figure below shows an m x n array represented in image-processing notation.

IDL’s choice of column-major array layout reflects its roots as an image processing language. The fact that the elements of the first dimension are contiguous means that the elements of each row of an image array (using [column, row] notation, as shown in the second figure, are contiguous. This is the order expected by most graphics hardware, providing an efficiency advantage for languages that naturally store data that way. Also, this ordering minimizes virtual memory overhead, since images are accessed linearly.

It should be clear that the higher-level meanings associated with array dimensions (row, column, latitude, longitude, etc.) are nothing more than a human notational device. In general, you can assign any meaning you wish to the dimensions of an array, and as long as your use of those dimensions is consistent, you will get the correct answer, regardless of the order in which IDL chooses to store the actual array elements in computer memory. Thus, it is usually possible to ignore these issues. There are times however, when understanding memory layout can be important:

Sharing Data With Other Languages

If binary data written by a row major language is to be input and used by IDL, transposition of the data is usually required first. Similarly, if IDL is writing binary data for use by a program written in a row major language, transposition of the data before writing (or on input by the other program) is often required.

Calling Code Written In Other Languages

When passing IDL data to code written in a row major language via dynamic linking (CALL_EXTERNAL, LINKIMAGE, DLMs), it is often necessary to transpose the data before passing it to the called code, and to transpose the results.

Matrix Multiplication

Understanding the difference between the IDL # and ## operators requires an understanding of array layout. For a discussion of how the ordering of such data relates to IDL mathematics routines, see Manipulating Arrays.

1-D Subscripting Of Multidimensional Array

IDL allows you to index multidimensional arrays using a single 1-D subscript. For example, given a two dimensional 5x7 array, ARRAY[2,3] and ARRAY[17] refer to the same array element. Knowing this requires an understanding of the actual array layout in memory (d2*m + d1, or 3*5+2, which yields 17).

Efficiency

Accessing memory in the wrong order can impose a severe performance penalty if your data is larger than the physical memory in your computer. Accessing elements of an array along the contiguous dimension minimizes the amount of memory paging required by the virtual memory subsystem of your computer hardware, and will therefore be the most efficient. Accessing memory across the non-contiguous dimension can cause each such access to occur on a different page of system memory. This forces the virtual memory subsystem into a cycle in which it must continually force current pages of memory to disk in order to make room for new pages, each of which is only momentarily accessed. This inefficient use of virtual memory is commonly known as thrashing.