The IMSL_BESSY function evaluates a Bessel function of the second kind with real order and real or complex parameters.
This routine requires an IDL Advanced Math and Stats license. For more information, contact your sales or technical support representative.
The IMSL_BESSY function evaluates a Bessel function of the second kind with real order and real or complex parameters. The data type of the returned value is always complex.
The Bessel function, Yv(Z), is defined as follows:
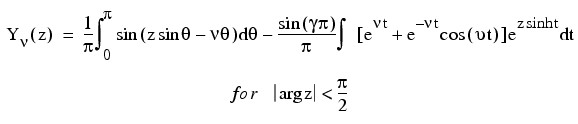
This function is based on the code BESSCC of Thompson (1981) and Thompson and Barnett (1987). This code computes Yv(z) from the modified Bessel functions Iv(z) and Kv(z), using the following relation:
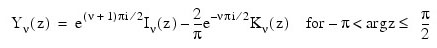
Example
In this example, Y0.3 + v–1(1.2 + 0.5i), v = 1, ..., 4 is computed and printed.
z = COMPLEX(1.2, .5)
FOR i = 0, 3 DO PM, IMSL_BESSY(i + .3, z) ( -0.0131453, 0.379593)
( -0.715533, 0.338082) ( -1.04777, 0.794969) ( -1.62487, 3.68447)
PM, IMSL_BESSY(.3, z, Sequence = 4), Title = 'With SEQUENCE:'
IDL prints:
With SEQUENCE:
( -0.0131453, 0.379593)
( -0.715533, 0.338082)
( -1.04777, 0.794969)
( -1.62487, 3.68447)
Syntax
Result = IMSL_BESSY(Order, Z [, /DOUBLE] [, SEQUENCE=value])
Return Value
The desired value of the modified Bessel function.
Arguments
Order
Real parameter specifying the desired order. The argument order must be greater than –1/2.
Z
Real or complex parameter for which the Bessel function is to be evaluated.
Keywords
DOUBLE (optional)
If present and nonzero, then double precision is used.
SEQUENCE (optional)
If present and nonzero, a one-dimensional array of length n containing the values of the Bessel function through the series is returned by IMSL_BESSY, where n = NELEMENTS(SEQUENCE). The i-th element of this array is the Bessel function of order (Order + i) at Z for i = 0, ... (n – 1).
Version History