The IMSL_ERF function evaluates the real error function erf (x). Using a keyword, the inverse error function erf –1(x) can be evaluated.
This routine requires an IDL Advanced Math and Stats license. For more information, contact your sales or technical support representative.
The error function erf(x) is defined below:
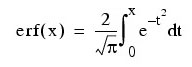
All values of x are legal. The inverse error function y = erf –1(x) is such that x = erf (y).
Examples
Example 1
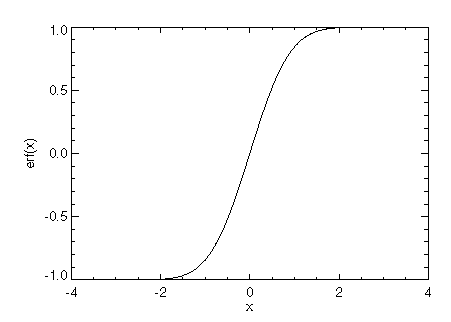
Plot the error function over [ –3, 3 ]. The results are shown in the figure that follows.
x = 6 * FINDGEN(100)/99 - 3
PLOT, x, IMSL_ERF(x), XTitle = 'x', YTitle = 'erf(x)'
Example 2
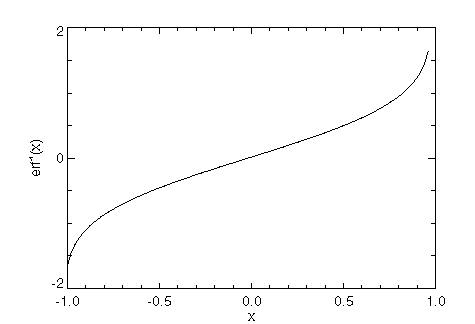
Plot the inverse of the error function over ( –1, –1). The results are shown in the next figure.
.
x = 2 * FINDGEN(100)/99 - 1
PLOT, x, IMSL_ERF(x(1:98), /Inverse), XTitle = 'x', $ YTitle = 'erf!E-1!N(x)'
Syntax
Result = IMSL_ERF(X [, /DOUBLE] [, /INVERSE]
Return Value
The value of the error function erf(x).
Arguments
X
Expression for which the error function is to be evaluated.
Keywords
DOUBLE (optional)
If present and nonzero, double precision is used.
INVERSE (optional)
Evaluates the real inverse error function erf–1(x). The inverse error function is defined only for –1 < x < 1.
Version History