The IMSL_FMINV function minimizes a function f(x) of n variables using a quasi-Newton method.
This routine requires an IDL Advanced Math and Stats license. For more information, contact your sales or technical support representative.
The IMSL_FMINV function uses a quasi-Newton method to find the minimum of a function f(x) of n variables. The problem is stated below:
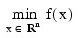
Given a starting point xc, the search direction is computed according to the formula:
d = –B–1gc
where B is a positive definite approximation of the Hessian and gc is the gradient evaluated at xc.
A line search is then used to find a new point:
xn = xc + λ d, λ > 0
such that:
f(xn) ≤ f(xc) α gTd
where α ∈ (0, 0.5 ) .
Finally, the optimality condition:
|| g(x) || ≤ ε
is checked, where ε is a gradient tolerance.
When optimality is not achieved, B is updated according to the BFGS formula:
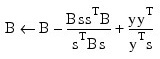
where s = xn – xc and y = gn – gc. Another search direction is then computed to begin the next iteration. For more details, see Dennis and Schnabel (1983, Appendix A).
In this implementation, the first stopping criterion for IMSL_FMINV occurs when the norm of the gradient is less than the given gradient tolerance TOL_GRAD. The second stopping criterion for IMSL_FMINV occurs when the scaled distance between the last two steps is less than the step tolerance TOL_STEP.
Since by default, a finite-difference method is used to estimate the gradient for some single-precision calculations, an inaccurate estimate of the gradient may cause the algorithm to terminate at a noncritical point. In such cases, high-precision arithmetic is recommended or keyword GRAD is used to provide more accurate gradient evaluation.
Examples
Example 1
The function f(x) = 100 (x2 – x12)2 + (1 – x1)2 is minimized.
.RUN
FUNCTION f, x
xn = x
xn(0) = x(1) - x(0)^2 xn(1) = 1 - x(0)
RETURN, 100 * xn(0)^2 + xn(1)^2
END
xmin = IMSL_FMINV('f', 2)
PM, xmin, Title = 'Solution:'
IDL prints:
Solution:
0.999986
0.999971
Continue:
PM, f(xmin), Title = 'Function value:'
IDL prints:
Function value:
2.09543e-10
Example 2
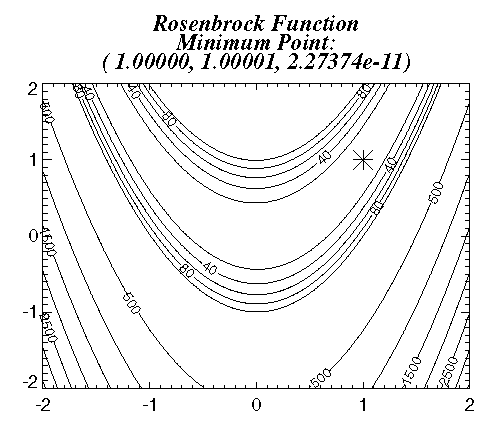
The function f(x) = 100 (x2 – x12)2 + (1 – x1)2 is minimized with the initial guess x = ( –1.2, 1.0). In the following plot, the asterisk marks the minimum. The results are shown in the plot below.
.RUN
FUNCTION f, x
xn = x
xn(0) = x(1) - x(0)^2 xn(1) = 1 - x(0)
RETURN, 100 * xn(0)^2 + xn(1)^2
END
.RUN
FUNCTION grad, x
g = x
g(0) = -400 * (x(1) - x(0)^2) * x(0) - 2 * (1 - x(0))
g(1) = 200 * (x(1) - x(0)^2) RETURN, g
END
xmin = IMSL_FMINV('f', 2, grad = 'grad',$
XGuess = [-1.2, 1.0], Tol_Grad = .0001)
x = 4 * FINDGEN(100)/99 - 2
y = x
surf = FLTARR(100, 100)
FOR i = 0, 99 DO FOR j = 0, 99 do $
surf(i, j) = f([x(i), y(j)])
str = '(' + STRCOMPRESS(xmin(0)) + ',' + $
STRCOMPRESS(xmin(1)) + ',' + STRCOMPRESS(f(xmin)) + ')'
!P.Charsize = 1.5
CONTOUR, surf, x, y, Levels = [20*FINDGEN(6), $
500 + FINDGEN(7)*500], /C_Annotation, $
Title='!18Rosenbrock Function!C' + 'Minimum Point:!C' + $
str, Position = [.1, .1, .8, .8]
OPLOT, [xmin(0)], [xmin(1)], Psym = 2, Symsize = 2
Result:
Errors
Informational Errors
MATH_STEP_TOLERANCE: Scaled step tolerance satisfied. Current point may be an approximate local solution, but it is also possible that the algorithm is making very slow progress and is not near a solution or that TOL_STEP is too big.
Warning Errors
MATH_REL_FCN_TOLERANCE: Relative function convergence. Both the actual and predicted relative reductions in the function are less than or equal to the relative function convergence tolerance.
MATH_TOO_MANY_ITN: Maximum number of iterations exceeded.
MATH_TOO_MANY_FCN_EVAL: Maximum number of function evaluations exceeded.
MATH_TOO_MANY_GRAD_EVAL: Maximum number of gradient evaluations exceeded.
MATH_UNBOUNDED: Five consecutive steps have been taken with the maximum step length.
MATH_NO_FURTHER_PROGRESS: Last global step failed to locate a point lower than the current x value.
Fatal Errors
MATH_FALSE_CONVERGENCE: Iterates appear to converge to a noncritical point. It is possible that incorrect gradient information is used, or the function is discontinuous, or the other stopping tolerances are too tight.
Syntax
Result = IMSL_FMINV(f, n [, /DOUBLE] [, GRAD=string] [, FSCALE=string] [, FVALUE=variable] [, IHESS=parameter] [, ITMAX=value] [, MAX_EVALS=value] [, MAX_GRAD=value] [, MAX_STEP=value] [, N_DIGIT=value] [, TOL_GRAD=value] [, TOL_RFCN=value] [, TOL_STEP=value] [, XGUESS=array] [, XSCALE=array])
Return Value
The minimum point x of the function. If no value can be computed, NaN is returned.
Arguments
f
Scalar string specifying a user-supplied function to evaluate the function to be minimized. Function f accepts the point at which the function is evaluated and returns the computed function value at the point.
n
Number of variables.
Keywords
DOUBLE (optional)
If present and nonzero, double precision is used.
GRAD (optional)
Scalar string specifying a user-supplied function to compute the gradient. The GRAD function accepts the point at which the gradient is evaluated and returns the computed gradient at the point.
FSCALE (optional)
Scalar containing the function scaling. The keyword FSCALE is used mainly in scaling the gradient. See the TOL_GRAD keyword for more detail. The default value is 1.0.
FVALUE (optional)
Name of a variable into which the value of the function at the computed solution is stored.
IHESS (optional)
Hessian initialization parameter. If IHESS is zero, the Hessian is initialized to the identity matrix; otherwise, it is initialized to a diagonal matrix containing max(f(t), fs) * si on the diagonal, where t = XGUESS, fs = FSCALE, and s = XSCALE. The default value is 0.
ITMAX (optional)
Maximum number of iterations. The default value is 100.
MAX_EVALS (optional)
Maximum number of function evaluations. The default value is 100 400.
MAX_GRAD (optional)
Maximum number of gradient evaluations. The default value is 100 400.
MAX_STEP (optional)
Maximum allowable step size. Default: 1000*max(ε1, ε2), where:
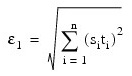
ε2 = || s ||2, s = XSCALE, and t = XGUESS
N_DIGIT (optional)
Number of good digits in function. Default: machine dependent.
TOL_GRAD (optional)
Scaled gradient tolerance.
The i-th component of the scaled gradient at x is calculated as:
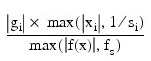
where:
- g = ∇f(x)
- s = XSCALE
- fs = FSCALE
Default: ε1/2 (ε1/3 in double), where ε is the machine precision.
TOL_RFCN (optional)
Relative function tolerance. The default is TOL_RFCN = max(10–10, ε 2/3), max(10–20, ε 2/3) in double.
TOL_STEP (optional)
Scaled step tolerance.
The i-th component of the scaled step between two points x and y is computed as:
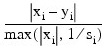
where s = XSCALE. Default: ε 2/3
XGUESS (optional)
Array with n components containing an initial guess of the computed solution. Default: XGUESS (*) = 0.
XSCALE (optional)
Array with n components containing the scaling vector for the variables. The keyword XSCALE is used mainly in scaling the gradient and the distance between
two points (see the keywords TOL_GRAD and TOL_STEP for more detail). Default: XSCALE (*) = 1.0.
Version History