The IMSL_GAMMAI function evaluates the incomplete gamma function γ(A, X).
This routine requires an IDL Advanced Math and Stats license. For more information, contact your sales or technical support representative.
The incomplete gamma function, γ(a, x), is defined as follows:
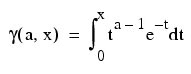
The incomplete gamma function is defined only for a > 0. Although γ(a, x) is well-defined for x > –infinity, this algorithm does not calculate γ(a, x) for negative x. For large a and sufficiently large x, γ(a, x) may overflow. Gamma function γ(a, x) is bounded by Γ(a), and users may find this bound a useful guide in determining legal values for a.
Example
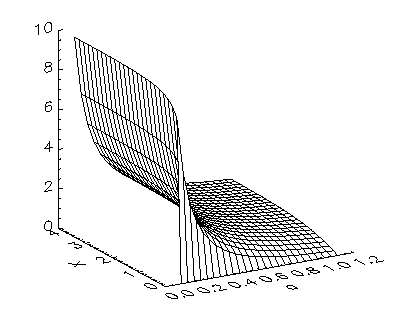
Plot the incomplete gamma function over [0.1, 1.1] x [0, 4]. The results are shown below.
x = 4. * FINDGEN(25)/24
a = 1e-1 + FINDGEN(25)/24 b = FLTARR(25, 25)
FOR i = 0, 24 DO b(i, *) = IMSL_GAMMAI(a(i), x)
!P.Charsize = 2.5
SURFACE, b, a, x, XTitle = 'a', YTitle = 'X'
Errors
Fatal Errors
MATH_NO_CONV_200_TS_TERMS: Function did not converge in 200 terms of Taylor series.
MATH_NO_CONV_200_CF_TERMS: Function did not converge in 200 terms of the continued fraction.
Syntax
Result = IMSL_GAMMAI(A, X [, /DOUBLE])
Return Value
The value of the incomplete gamma function γ(a, x).
Arguments
A
Integrand exponent parameter. It must be positive.
X
Upper limit of integration. It must be nonnegative.
Keywords
DOUBLE (optional)
If present and nonzero, double precision is used.
Version History
See Also
IMSL_GAMMACDF