This version of the IMSL_INTFCN function integrates functions using a globally adaptive scheme based on Gauss-Kronrod rules. To use this integration method, supply the RULE keyword.

This routine requires an IDL Advanced Math and Stats license. For more information, contact your sales or technical support representative.

This method is a general-purpose integrator that uses a globally adaptive scheme to reduce the absolute error. It subdivides the interval [a, b] and uses a (2k+1)-point Gauss-Kronrod rule to estimate the integral over each subinterval. The error for each subinterval is estimated by comparison with the k-point Gauss quadrature rule. The subinterval with the largest estimated error is then bisected, and the same procedure is applied to both halves. The bisection process is continued until either the error criterion is satisfied, roundoff error is detected, the subintervals become too small, or the maximum number of subintervals allowed is reached. This method is based on the subroutine QAG by Piessens et al. (1983).

If this method is used, the function should be coded to protect endpoint singularities if they exist.

Example

The value of:

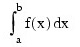
is computed. Since the integrand is oscillatory, RULE = 6 is used. The exact value is 0.50406706. The values of the actual and estimated error are machine dependent.

.RUN
; Define the function to be integrated.
FUNCTION f, x
  RETURN, SIN(1/x)
END
ans = IMSL_INTFCN('f', 0, 1, RULE=6)
 
; Call IMSL_INTFCN, to compute the integral based on
; the specified Gauss-Kronrod rule.
PM, 'Computed Answer:',ans

IDL prints:

Computed Answer:
  0.504051
  exact = .50406706
 
PM, 'EXACT - COMPUTED:', exact - ans

IDL prints:

Exact - Computed:
  1.62125e-05

Errors

See IMSL_INTFCN Errors.

Syntax

Result = IMSL_INTFCN(F, A, B, RULE = {1-6} [, RULE=value])

Return Value

An estimate of the desired integral. If no value can be computed, the floating-point value NaN (Not a Number) is returned.

Arguments

F

A scalar string specifying the name of a user-supplied function to be integrated. The function f accepts one scalar parameter and returns a single scalar of the same type.

A

A scalar expression specifying the lower limit of integration.

B

A scalar expression specifying the upper limit of integration.

Keywords

In addition to the global IMSL_INTFCN keywords, the following keyword is available:

RULE (optional)

Set this keyword equal to an integer representing the Gauss-Kronrod rule to use. Possible values are:

Rule

Gauss-Kronrod Rule

1

7-15 points

2

10-21 points

3

15-31 points

4

20-41 points

5

25-51 points

6

30-61 points

Version History

6.4

Introduced

See Also

IMSL_INTFCN