The IMSL_LNBETA function evaluates the logarithm of the real beta function ln β(x, y).
This routine requires an IDL Advanced Math and Stats license. For more information, contact your sales or technical support representative.
The beta function, β(x, y), is defined as:
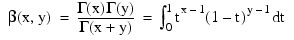
and IMSL_LNBETA returns ln β(x, y). The logarithm of the beta function requires that x > 0 and y > 0. It can overflow for very large parameters.
Example
Evaluate the log of the beta function ln β (0.5, 0.2).
PM, IMSL_LNBETA(.5, .2)
1.83556
Errors
Warning Errors
MATH_X_IS_TOO_CLOSE_TO_NEG_1: Result is accurate to less than one precision because the expression –x / (x + y) is too close to –1.
Syntax
Result = IMSL_LNBETA(x, y [, /DOUBLE])
Return Value
The value of the logarithm of the beta function β(x, y).
Arguments
X
First argument of the beta function. It must be positive.
Y
Second argument of the beta function. It must be positive.
Keywords
DOUBLE (optional)
If present and nonzero, double precision is used.
Version History