The IMSL_SMOOTHDATA1D function smooths one-dimensional data by error detection.
This routine requires an IDL Advanced Math and Stats license. For more information, contact your sales or technical support representative.
The IMSL_SMOOTHDATA1D function is designed to smooth a data set that is mildly contaminated with isolated errors. In general, the routine will not work well if more than 25% of the data points are in error. The routine IMSL_SMOOTHDATA1D is based on an algorithm of Guerra and Tapia (1974).
Setting N_ELEMENTS(x) = n, Y = f, Result = s and X= x, the algorithm proceeds as follows. Although the user need not an ordered x sequence, we will assume that x is increasing for simplicity. The algorithm first sorts the x values into an increasing sequence and then continues. A cubic spline interpolant is computed for each of the 6-point data sets (initially setting s = f ):
(xj, sj) j = i – 3, ... , i + 3 j ≠ i
where i = 4, ... , n – 3. For each i the interpolant, which we will call Si, is compared with the current value of si, and a `point energy' is computed as:
pei = Si(xi) – si
Setting sc = SC, the algorithm terminates either if ITMAX iterations have taken place or if:
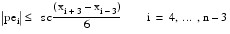
If the above inequality is violated for any i, then we update the i-th element of s by setting si = si + d(pei), where d = DISTANCE. Note that neither the first three nor the last three data points are changed. Thus, if these points are inaccurate, care must be taken to interpret the results.
The choice of the parameters DISTANCE, SC and ITMAX are crucial to the successful usage of this subroutine. If the user has specific information about the extent of the contamination, then he should choose the parameters as follows: DISTANCE = 1, SC = 0 and ITMAX to be the number of data points in error. On the other hand, if no such specific information is available, then choose DISTANCE = 0.5, ITMAX ≤ 2n, and:
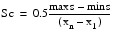
In any case, experimenting with these values is encouraed.
Example
We take 91 uniform samples from the function 5 + (5 + t2 sin t )/t on the interval
[1, 10]. First, define function F from which samples will be taken
FUNCTION F, xdata
RETURN, (xdata*xdata*SIN(xdata) + 5)/xdata + 5
END
Next, we contaminate 10 of the samples and try to recover the original function values.
isub = [5, 16, 25, 33, 41, 48, 55, 61, 74, 82]
rnoise = [2.5, -3.0, -2.0, 2.5, 3.0, -2.0, -2.5, 2.0, -2.0, 3.0]
sc = 0.56 itmax = 182
xdata = 1 + 0.1*FINDGEN(91)
fdata = f(xdata)
fdata(isub) = fdata(isub) + rnoise
sdata = IMSL_SMOOTHDATA1D(xdata, fdata, Itmax = itmax, $
Distance = dis, Sc = sc)
PM, [[f(xdata(isub))], [fdata(isub)], [sdata(isub)]], $
Title = ' F(X) F(X) + noise sdata'
F(X) F(X) + noise sdata
9.82958 12.3296 9.87030
8.26338 5.26338 8.21537
5.20083 3.20083 5.16823
2.22328 4.72328 2.26399
1.25874 4.25874 1.30825
3.16738 1.16738 3.13830
7.16751 4.66751 7.13076
10.8799 12.8799 10.9092
12.7739 10.7739 12.7075
7.59407 10.5941 7.63885
dis = 1.0 sc = 0.0 itmax = 10.0
sdata = IMSL_SMOOTHDATA1D(xdata, fdata, Itmax = itmax, $
Distance = dis, Sc = sc)
% IMSL_SMOOTHDATA1D: Warning: MATH_ITMAX_EXCEEDED
PM, [[f(xdata(isub))], [fdata(isub)], [sdata(isub)]], $
Title = ' F(X) F(X) + noise sdata'
F(X) F(X) + noise sdata
9.82958 12.3296 9.83127
8.26338 5.26338 8.26223
5.20083 3.20083 5.19946
2.22328 4.72328 2.22495
1.25874 4.25874 1.26142
3.16738 1.16738 3.16958
7.16751 4.66751 7.16986
10.8799 12.8799 10.8779
12.7739 10.7739 12.7699
7.59407 10.5941 7.59194
Errors
Warning Errors
MATH_MAX_ITERATIONS_REACHED: Maximum number of iterations has been reached. The best approximation is returned.
Fatal Errors
MATH_DUPLICATE_XDATA_VALUES: The xdata values must be distinct.
MATH_NEGATIVE_WEIGHTS: All weights must be greater than or equal to zero.
Syntax
Result = IMSL_SMOOTHDATA1D(X, Y [, DISTANCE=value] [, /DOUBLE] [, ITMAX=value] [, SC=value])
Return Value
One-dimensional array containing the smoothed data.
Arguments
X
One-dimensional array containing the abscissas of the data points.
Y
One-dimensional array containing the ordinates of the data points.
Keywords
DISTANCE (optional)
Proportion of the distance the ordinate in error is moved to its interpolating curve. It must be in the range 0.0 to 1.0. Default: 1.0
DOUBLE (optional)
If present and nonzero, double precision is used.
ITMAX (optional)
The maximum number of iterations allowed. Default: 500
SC (optional)
The stopping criterion. SC should be greater than or equal to zero. Default: S0.0
SMPAR (optional)
Specifies the real, scalar smoothing parameter explicitly. See the description at the beginning of this topic for more details.
WEIGHTS (optional)
Array containing the weights to be used in the problem. Default: all weights are equal to 1.
Version History