Dates and times are among the many types of information that numerical data can represent. IDL provides a number of routines that offer specialized support for generating, analyzing, and displaying date- and time-based data (herein referred to as date/time data).
Julian Dates and Times
Within IDL, dates and times are typically stored as Julian dates. A Julian date is defined to be the number of days elapsed since noon on January 1, 4713 BCE. Following the astronomical convention, a Julian day is defined to start at 12pm (noon). The Julian calendar, established by Julius Caesar in the year 45 BCE, was corrected by Pope Gregory XIII in 1582, excising ten days from the calendar. For dates after 4 October 1582, the calendar specifies that every 4 years is a leap year, except if the year ends in a "00" then it is not a leap year, unless it is also divisible by 400 (in which case it is a leap year).
The following table shows a few examples of calendar dates and their corresponding Julian dates.
|
Calendar Date |
Julian Date |
|
January 1, 4713 B.C.E., at 12pm
|
0 |
|
January 2, 4713 B.C.E., at 12pm
|
1 |
|
January 1, 2000 at 12pm
|
2451545 |
Julian dates can also include fractional portions of a day, thereby incorporating hours, minutes, and seconds. If the day fraction is included in a Julian date, it is represented as a double-precision floating point value. The day fraction is computed as follows:
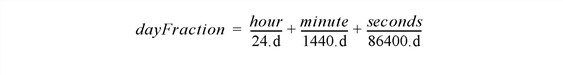
One advantage of using Julian dates to represent dates and times is that a given date/time can be stored within a single variable (rather than storing the year, month, day, hour, minute, and second information in six different variables). Because each Julian date is a number, IDL’s numerical routines can be applied to Julian dates just as for any other type of number.
The JULDAY and CALDAT routines can be used to convert to and from Julian Dates.
Proleptic Gregorian Calendar
IDL can also compute dates using the proleptic Gregorian calendar, which is produced by extending the Gregorian calendar backwards to dates preceeding its introduction in 1582. In the proleptic Gregorian calendar, there are no missing days in October 1582, every 4 years is a leap year, except if the year ends in a "00" then it is not a leap year, unless it is also divisible by 400 (in which case it is a leap year).
The proleptic Gregorian calendar is usually required for information exchange between international partners, as defined by ISO 8601:2004 (clause 3.2.1). The proleptic Gregorian calendar is not used by astronomers, who instead use the Julian Day Number, as given by the JULDAY function.
Note that there is no year 0 in the calendar as defined by IDL. Instead, year 1 CE is immediately preceded by year 1 BCE. This means that leap years are offset by 1. For example, -1, -5, -9, -13, etc. are all leap years, -101 is not a leap year (following the rule for "00" years), but -401 is a leap year.
The GREG2JUL and JUL2GREG routines can be used to convert to and from proleptic Gregorian dates.
Note: The JUL2GREG procedure should only be used with the GREG2JUL function. Similarly, the JULDAY function should only be used with CALDAT. For dates between 1 Jan CE and 15 Oct 1582 the two calendar systems differ by up to 10 days. For dates on or after 15 Oct 1582 the two calendar systems are identical.
|
Proleptic Gregorian Range
|
Julian Range |
Gregorian Ahead By
|
|
1 March 1 BCE to 26 Feb 100 CE
|
3 March 1 BCE to 28 Feb 100 CE
|
-2 days |
|
1 March 100 to 27 Feb 200
|
2 March 100 to 28 Feb 200
|
-1 days |
|
1 March 200 to 28 Feb 300
|
1 March 200 to 28 Feb 300
|
0 days |
|
2 March 300 to 28 Feb 500
|
1 March 300 to 27 Feb 500
|
1 day |
|
3 March 500 to 28 Feb 600
|
1 March 500 to 26 Feb 600
|
2 days
|
|
4 March 600 to 28 Feb 700
|
1 March 600 to 25 Feb 700
|
3 days |
|
5 March 700 to 28 Feb 900
|
1 March 700 to 24 Feb 900
|
4 days |
|
6 March 900 to 28 Feb 1000
|
1 March 900 to 23 Feb 1000
|
5 days |
|
7 March 1000 to 28 Feb 1100
|
1 March 1000 to 22 Feb 1100
|
6 days |
|
8 March 1100 to 28 Feb 1300
|
1 March 1100 to 21 Feb 1300
|
7 days |
|
9 March 1300 to 28 Feb 1400
|
1 March 1300 to 20 Feb 1400
|
8 days |
|
10 March 1400 to 28 Feb 1500
|
1 March 1400 to 19 Feb 1500
|
9 days |
|
11 March 1500 to 4 Oct 1582
|
1 March 1500 to 24 Sept 1582
|
10 days |
|
15 Oct 1582 to present
|
15 Oct 1582 to present
|
0 days |
Precision of Date/Time Data
The precision of any numerical value is defined as the smallest possible number that can be added to that value that produces a new value different from the first. Precision is typically limited by the data type of the variable used to store the number and the magnitude of the number itself. Within IDL, the following guide should be used when choosing a data format for date/time data:
- Time values that require a high precision, and that span a range of a few days or less, should be stored as double-precision values in units of “time elapsed” since the starting time, rather than in Julian date format. An example would be the “seconds elapsed” since the beginning of an experiment. In this case, the data can be treated within IDL as standard numeric data without the need to utilize IDL’s specialized date/time features.
- Date values that do not include the time of day may be stored as long-integer Julian dates. The Julian date format has the advantage of being compact (one value per date) and being evenly spaced in days. As an example, January 1st for the years 2000, 2001, and 2002 can be stored as Julian days 2451545, 2451911, and 2452276. The precision of this format is 1 day.
- Date values where it is necessary to include the time of day can be stored as double-precision Julian dates, with the time included as a day fraction. Because of the large magnitude of the Julian date (such as Julian day 2451545 for 1 January 2000), the precision of most Julian dates is limited to 1 millisecond (0.001 seconds).
To determine the precision of a Julian date/time value, you can use the IDL MACHAR function:
julian = JULDAY(1,1,2000,12,15,0)
machine = MACHAR(/DOUBLE)
precision = julian*machine.eps
PRINT, precision*86400d0
How to Generate Date/Time Data
The TIMEGEN function returns an array of double precision floating point values that represent date/time in terms of Julian dates. The first value of the returned array corresponds to a start date/time, and each subsequent value corresponds to the start date/time plus that array element's one-dimensional subscript multiplied by a step size for a given date/time unit. Unlike the other array generation routines in IDL, TIMEGEN includes a START keyword, which is necessary if the starting date/time is originally provided in calendar (month, day, year) form.
The following example begins with a start date of March 1, 2000 and increments every month for a full year:
date_time = TIMEGEN(12, UNIT = 'Months', $
START = JULDAY(3, 1, 2000))
where the UNIT keyword is set to 'Months' to increment by month and the START keyword is set to the Julian date form of March 1, 2000. The results of the above call to TIMEGEN can be output using either of the following methods:
-
Using the CALDAT procedure to convert the Julian dates to calendar dates:
CALDAT, date_time, month, day, year
FOR i = 0, (N_ELEMENTS(date_time) - 1) DO PRINT, $
month[i], day[i], year[i], $
FORMAT = '(i2.2, "/", i2.2, "/", i4)'
-
Using the calendar format codes:
PRINT, date_time, format = '(C(CMOI2.2, "/", CDI2.2, "/", CYI))'
The resulting calendar dates are printed out as follows:
03/01/2000
04/01/2000
05/01/2000
06/01/2000
07/01/2000
08/01/2000
09/01/2000
10/01/2000
11/01/2000
12/01/2000
01/01/2001
02/01/2001
The TIMEGEN routine contains several keywords to provide specific date/time data generation.
The TIMESTAMP function returns one or more date/time strings in ISO-8601 format, when you provide a year, month, day, hour, minute, second, and offset from Coordinated Universal Time (UTC).
The TIMESTAMPTOVALUES procedure is the inverse to TIMESTAMP. It passes through the year, month, day, hour, minute, second, and offset from Coordinated Universal Time (UTC), given a date/time string in ISO-8601 format.
Date/Time Data Examples
You can display date/time data on IDLgrAxis objects (through the TICKFORMAT property) plots, contours, and surfaces by setting tick mark attributes.