The IMSL_BESSK_EXP function evaluates the exponentially scaled modified Bessel function of the third kind of orders zero and one.

This routine requires an IDL Advanced Math and Stats license. For more information, contact your sales or technical support representative.

If the argument Order is zero, the Bessel function K₀(x) is defined to be:

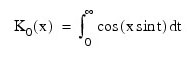
If order is one, the value of the Bessel function K1(x):

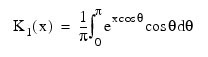
The argument X must be greater than zero for the result to be defined.

Example

---

The expression:

is computed directly by calling IMSL_BESSK_EXP, and indirectly by calling IMSL_BESSK. The absolute difference is printed. For large x, the internal scaling provided by IMSL_BESSK_EXP avoids underflow that may occur in IMSL_BESSK.

ans = IMSL_BESSK_EXP(0, 0.5)

error = ABS(ans - (EXP(0.5))*IMSL_BESSK(0, 0.5)) PRINT, ans

  1.52411

PRINT, 'Error =', error

IDL prints:

Error = 1.1920929e-07

Errors

---

Fatal Errors

MATH_SMALL_ARG_OVERFLOW: The argument X must be large enough (X > max (1/b, s) where s is the smallest representable positive number and b is the largest representable number) that K1(X) does not overflow.

Syntax

---

Result = IMSL_BESSK_EXP(Order, X [, /DOUBLE])

Return Value

---

The value of the exponentially scaled Bessel function e^xK₀(x) or e^xK₁(x)

Arguments

---

Order

Order of the function. The order must be either zero or one.

X

Argument for which the function value is desired.

Keyword

---

DOUBLE (optional)

If present and nonzero, then double precision is used.

Version History

---

6.4	Introduced

See Also

---

IMSL_BESSK