IMSL_BETA

The IMSL_BETA function evaluates the real beta function β(X, Y).

This routine requires an IDL Advanced Math and Stats license. For more information, contact your sales or technical support representative.

The beta function, β(x, y), is defined as:

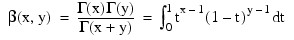
requiring that X > 0 and Y > 0. It underflows for large parameters.

Example

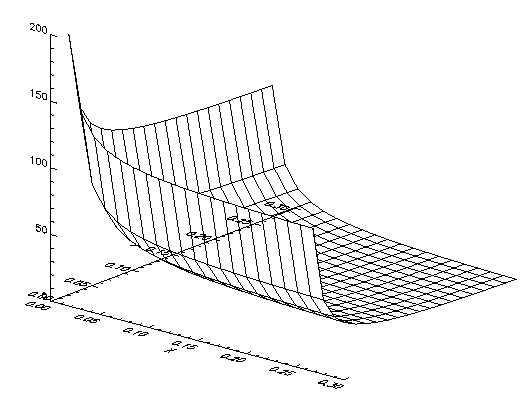
Plot the beta function over [ε, 1/4 + ε] x [ε, 1/4 + ε] for ε = 0.01. The results are shown in the Real Beta Function Plot after the code example.

x = 1e-2 + .25 * FINDGEN(25)/24 y = x

b = FLTARR(25, 25)

FOR i = 0, 24 DO b(i, *) = IMSL_BETA(x(i), y)

; Compute values of the beta function.

SURFACE, b, x, y, XTitle = 'X', YTitle = 'Y', Az = 320, ZAxis = 2

; Plot the computed values as a surface and rotate the plot.

MATH_BETA_UNDERFLOW: Parameters must not be so large that the result underflows.

MATH_ZERO_ARG_OVERFLOW: One of the parameters is so close to zero that the result overflows.

Result = IMSL_BETA(X, Y [, /DOUBLE])

The value of the beta function β(x, y). If no result can be computed, then NaN (Not a Number) is returned.

First beta parameter. It must be positive.

Second beta parameter. It must be positive.

If present and nonzero, double precision is used.

6.4	Introduced