The IMSL_ELRJ function evaluates Carlson’s elliptic integral of the third kind RJ (x, y, z, ρ).
This routine requires an IDL Advanced Math and Stats license. For more information, contact your sales or technical support representative.
Carlson’s elliptic integral of the third kind is defined to be:
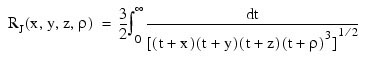
The arguments must be nonnegative. In addition, x + y, x + z, y + z and ρ must be greater than or equal to (5s)1/3 and less than or equal to 0.3(b/5)1/3, where s is the smallest representable floating-point number. Should any of these conditions fail IMSL_ELRJ is set to b, the largest floating-point number.
The IMSL_ELRJ function is based on the code by Carlson and Notis (1981) and the work of Carlson (1979).
Example
The integral RJ (2, 3, 4, 5) is computed.
PRINT, IMSL_ELRJ(2.0, 3.0, 4.0, 5.0)
0.142976
Syntax
Result = IMSL_ELRJ(X, Y, Z, Rho [, /DOUBLE]
Return Value
The complete elliptic integral RJ (x, y, z, ρ).
Arguments
Rho
Fourth argument for which the function value is desired. It must be positive.
X
First argument for which the function value is desired. It must be nonnegative.
Y
Second argument for which the function value is desired. It must be nonnegative.
Z
Third argument for which the function value is desired. It must be positive.
Keywords
DOUBLE (optional)
If present and nonzero, double precision is used.
Version History