The IMSL_ELK function evaluates the complete elliptic integral of the kind K(x).
This routine requires an IDL Advanced Math and Stats license. For more information, contact your sales or technical support representative.
The complete elliptic integral of the first kind is defined to be:
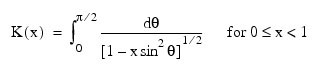
The argument x must satisfy 0 ≤ x < 1; otherwise, IMSL_ELK returns the largest representable floating-point number.
The function K(x) is computed using IMSL_ELRF and the relation K(x) = RF(0, 1 − x, 1).
Example
The integral K(0) is evaluated.
PRINT, IMSL_ELK(0.0)
1.57080
Syntax
Result = IMSL_ELK(X [, /DOUBLE]
Return Value
The complete elliptic integral K(x).
Arguments
X
Argument for which the function value is desired.
Keywords
DOUBLE (optional)
If present and nonzero, double precision is used.
Version History
See Also
IMSL_ELRF