The IMSL_DIFFERENCE function differences a seasonal or nonseasonal time series.
This routine requires an IDL Advanced Math and Stats license. For more information, contact your sales or technical support representative.
The IMSL_DIFFERENCE function performs m = N_ELEMENTS(Periods) successive backward differences of period si = Periods(i – 1) and di = Orders(i – 1) for i = 1, ..., m on the n = N_ELEMENTS(x) observations {Zt} for t = 1, 2, ..., n.
Consider the backward shift operator B given by:
BkZt = Zt – k
for all k. Then, the backward difference operator with period s is defined by the following:
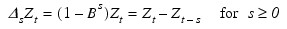
Note that BsZt and ∆sZt are defined only for t = (s + 1), ..., n. Repeated differencing with period s is simply:
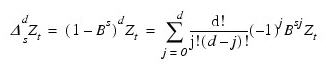
where d ≥ 0 is the order of differencing. Note that ∆ds Zt is defined only for t = (sd + 1), ..., n.
The general difference formula used in IMSL_DIFFERENCE is given by:
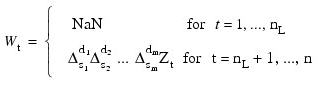
where nL represents the number of observations “lost” because of differencing and NaN represents the missing value code. See IMSL_MACHINE to retrieve missing values. Note that:
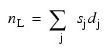
A homogeneous, stationary time series can be arrived at by appropriately differencing a homogeneous, nonstationary time series (Box and Jenkins 1976, p. 85). Preliminary application of an appropriate transformation followed by differencing of a series enables model identification and parameter estimation in the class of homogeneous stationary IMSL_ARMA.
Examples
Example 1
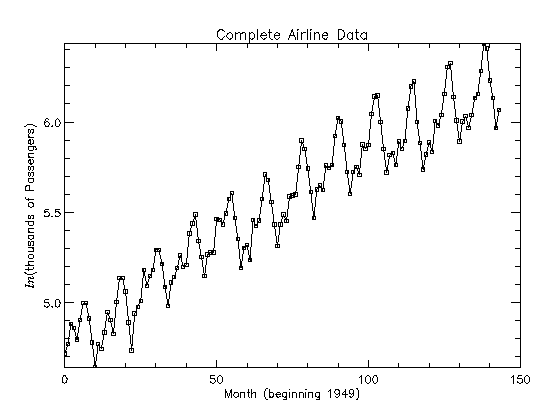
Consider the Airline Data (Box and Jenkins 1976, p. 531) consisting of the monthly total number of international airline passengers from January 1949 through December 1960. The entire data, after taking a natural logarithm, are shown in the plot below. The plot shows a linear trend and a seasonal pattern with a period of 12 months. This suggests that the data needs a nonseasonal difference operator, ∆1, and a seasonal difference operator, ∆12, to make the series stationary. The IMSL_DIFFERENCE function is used to compute:
Wt = ∆1∆12Zt = (Zt – Zt – 12) – (Zt – 1 – Zt – 13)
for t = 14, 15, ..., 24.
ztemp = ALOG(IMSL_STATDATA(4))
PLOT, INDGEN(144), ztemp, Psym = -6, Symsize = .5, $
YStyle = 1, Title = 'Complete Airline Data', $
XTitle = 'Month (beginning 1949)', $
YTitle = '!8ln!3(thousands of Passengers)'
periods = [1, 12]
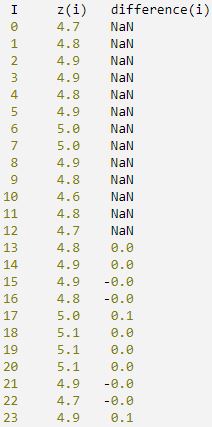
difference = IMSL_DIFFERENCE(z, periods)
matrix = [[INDGEN(24)], [z], [difference]]
PM, matrix, FORMAT = '(i4, x, 2f7.1)', $
Title = ' I z(i) difference(i)'
IDL prints:
Example 2
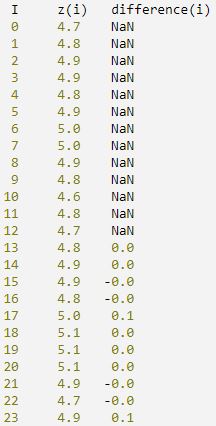
The data for this example is the same as that for the initial example. The first NUM_LOST observations are excluded from W due to differencing, and NUM_LOST also is output.
ztemp = ALOG(IMSL_STATDATA(4))
z = ztemp(0:23)
periods = [1, 12]
diff = IMSL_DIFFERENCE(z, periods, $
/EXCLUDE_FIRST, NUM_LOST = num_lost)
num_valid = N_ELEMENTS(z) - num_lost
matrix = [[INDGEN(num_valid)], [z(0:num_valid-1)], $
[DIFF(0:num_valid-1)]]
PM, matrix, FORMAT = '(i4, x, 2f7.1)', $
TITLE = ' i z(i) IMSL_DIFFERENCE(i)'
Result:
Errors
Fatal Errors
STAT_PERIODS_LT_ZERO: Parameter periods (#) = #. All elements of Periods must be greater than zero.
STAT_ORDER_NEGATIVE: Parameter order (#) = #. All elements of order must be nonnegative.
STAT_Z_CONTAINS_NAN: Parameter z (#) = NaN; Z cannot contain missing values. Other elements of Z may be equal to NaN.
Syntax
Result = IMSL_DIFFERENCE(Z, Periods [, /DOUBLE] [, /EXCLUDE_FIRST] [, /FIRST_TO_NAN] [, NUM_LOST=variable] [, ORDERS=array])
Return Value
One-dimensional array of length N_ELEMENTS (Z) containing the differenced series.
Arguments
Z
One-dimensional array containing the time series.
Periods
One-dimensional array containing the periods at which Z is to be differenced.
Keywords
DOUBLE (optional)
If present and nonzero, double precision is used.
EXCLUDE_FIRST (optional)
If EXCLUDE_FIRST is set to a nonzero value, the first NUM_LOST observations are excluded from the solution due to differencing. The differenced series is of length N_ELEMENTS(Periods) – NUM_LOST. If FIRST_TO_NAN is specified, the first NUM_LOST observations are set to NaN (Not a Number). This is the default if neither EXCLUDE_FIRST nor FIRST_TO_NAN is specified.
FIRST_TO_NAN (optional)
If EXCLUDE_FIRST is present and nonzero, the first NUM_LOST observations are excluded from the solution due to differencing. The differenced series is of length N_ELEMENTS(Periods) – NUM_LOST. If FIRST_TO_NAN is specified, the first NUM_LOST observations are set to NaN (Not a Number). This is the default if neither EXCLUDE_FIRST nor FIRST_TO_NAN is specified.
NUM_LOST (optional)
Named variable into which the number of observations "lost" because of differencing the time series Z is stored.
ORDERS (optional)
One-dimensional array of length N_ELEMENTS(Periods) containing the order of each difference given in periods. The elements of ORDERS must be greater than or equal to 0. The default behavior is that all elements equal 1.
Version History