The IMSL_KELVIN_BEI0 function evaluates the Kelvin function of the first kind, bei, of order zero.

This routine requires an IDL Advanced Math and Stats license. For more information, contact your sales or technical support representative.

The Kelvin function bie₀(x) is defined to be 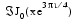. The Bessel function J₀(x) is defined:

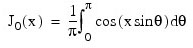
In IMSL_KELVIN_BEI₀, x must be less than 119.

If the keyword DERIVATIVE is set, the function bei0′(x) is defined to be:

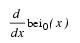
If the keyword DERIVATIVE is set and |x| > 119, NaN is returned.

The IMSL_KELVIN_BEI0 function is based on the work of Burgoyne (1963).

Example

---

In this example, bei₀(0.4) and bei₀′(0.6) are evaluated.

PRINT, IMSL_KELVIN_BEI0(0.4)

  0.0399982

PRINT, IMSL_KELVIN_BEI0(0.6, /DERIVATIVE)

  0.299798

Syntax

---

Result = IMSL_KELVIN_BEI0(X [, DERIVATIVE=value] [, /DOUBLE])

Return Value

---

The value of the Kelvin function of the first kind, bei, of order zero evaluated at x.

Arguments

---

X

Argument for which the function value is desired.

Keywords

---

DERIVATIVE (optional)

If present and nonzero, then the derivative of the Kelvin function of the first kind, bei, of order zero evaluated at x is computed.

DOUBLE (optional)

If present and nonzero, then double precision is used.

Version History

---

6.4	Introduced

See Also

---

IMSL_KELVIN_BER0, IMSL_KELVIN_KEI0, IMSL_KELVIN_KER0